CS 3710

Introduction to Cybersecurity

Aaron Bloomfield (aaron@virginia.edu)
@github | ↑ |

Encryption

Introduction

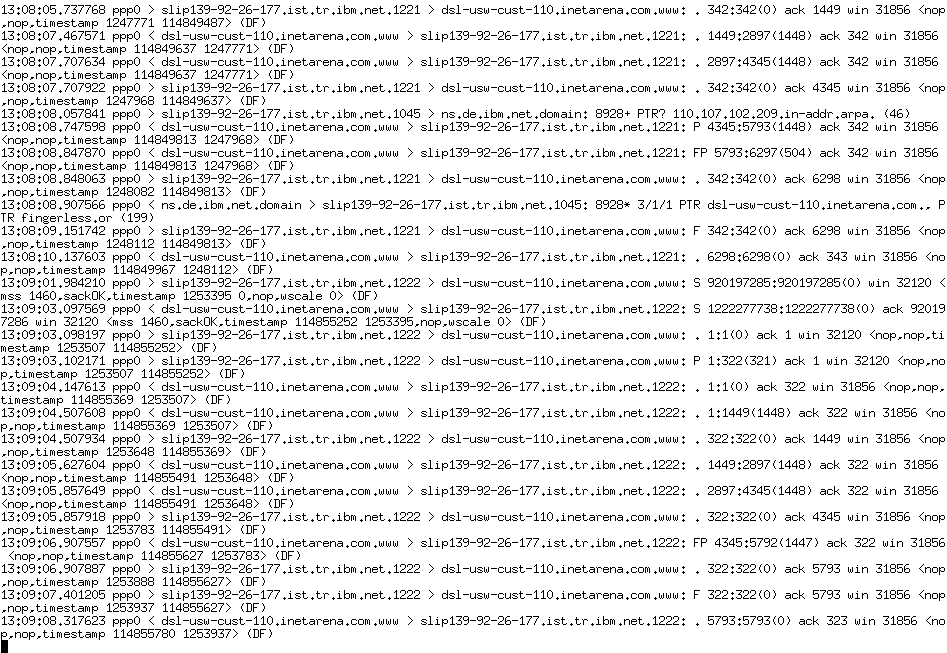
Telnet and tcpdump

Telnet is the old version of ssh (aka SecureCRT), and sends all data as plaintext
tcpdump will dump all data sent over a TCP/IP interface
The next slide shows a tcpdump
- … but without the data in the packets, which has been eliminated from this slide
It’s easy to show that data, though

Codes versus Ciphers

Codes change the meaning of words, ciphers encrypt them
Coded messages:
- “The light is on in the attic”
Cipher’ed messages:
- wkh txlfn eurzq ira mxpsv ryhu wkh odcb grj
- wecrl teerd soeef eaoca ivden
Reference

Codes

One- and two-part codes: contains one or two books that correlate coded words with their plaintext meanings
One-time code: a pre-arranged word or phrase intended to be used only once, and to convey a message
- “Over all of Spain, the sky is clear” - over the radio, it started the Spanish revolt of 1936

Codes

Idiot code: any sentence with ‘day’ and ‘night’ means ‘attack’ the location in the sentence
- Plaintext: Attack Gotham.
- Codetext: We walked day and night through the streets but couldn’t find it! Tomorrow we’ll head into Gotham.
Reference

Security through obscurity

The use of secrecy to hide the cryptographic system being used
- Contrast this with algorithms such as RSA, which are publically analyzed
The problems is that somebody will figure out how it works (“many eyes make all bugs shallow” - Linus Torvalds)
- And then, if there is a flaw (due to lack of peer review), the system is vulnerable
Reference

Block-ciphers vs. stream ciphers

Block ciphers require a block of text (perhaps 1 Kb, for example)
- Reference
Stream ciphers encrypt data as it is provided, character-by-character
- I prefer the name ‘character cipher’ over ‘stream cipher’
- Reference

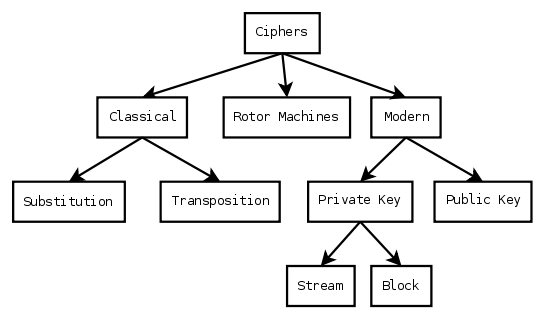
Cipher Taxonomy

cipher taxonomy - Reference

Classical ciphers and rotor machines

Caesar Cipher

Julius Caesar used it to send military messages
- Rome’s enemies were unable to crack it!
A simple substitution cipher
- Encryption: replace any letter with the letter 3 spots beyond
Decryption: the same, but go 3 letters back

Caesar Cipher

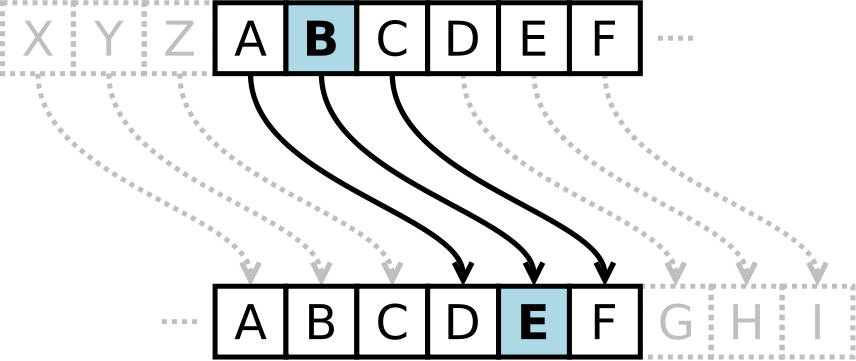
Caesar Cipher analysis

Example:
- Plaintext: the quick brown fox jumps over the lazy dog
- Ciphertext: WKH TXLFN EURZQ IRA MXPSV RYHU WKH ODCB GRJ
Pros:
- Easy to encrypt and decrypt by hand
Cons:
- Easy to crack by hand

Caesar Cipher analysis

Cracking
- There are only 26 possibilities!
  - Well, 25 really – nobody would encrypt with a key of 0 or 26…
- A program could do this in a matter of microseconds; a person in a matter of minutes
- Example: crack “s psxn iyeb vkmu yp pksdr nscdeblsxq” online here (select ‘bruteforce’)
Substitution ciphers can be more complex
- Having a mapping, rather than a rotation

Cracking a substitution cipher

Cracking a Caesar cipher is trivial
- There are only 26 possibilities
But what about a more general substitution cipher?
Letter frequency analysis
- ‘e’ is the most common letter (12.7%)
- ‘z’ is the least common letter (0.1%)
- Reference
Still very easy to crack

Vigenere cipher

If a Caesar Cipher is a alphabetic substitution, then a Vigenere cipher is a poly-alphabetic substitution cipher
The table used is the shown on the next slide
Suppose the message to encrypt is “attackatdawn”
And the keyword is “lemon”

Vigenere cipher table

Vigenere cipher

Cipher algorithm:
- Repeat the keyword until it matches the length of the message
  - “attackatdawn” is 12 letters; the new keyword is “lemonlemonle”
- Encrypt the first letter of the message using the first letter of the keyword, etc.
  - ‘a’ is encrypted with ‘l’, ‘t’ with ‘e’, etc.
- The encryption is done by finding the row of the message character, and the column of the keyword

Vigenere cipher

vigenere table Encrypt “attackatdawn” with “lemon”

Vigenere cipher result

Plaintext: ATTACKATDAWN
Key: LEMONLEMONLE
Ciphertext: LXFOPVEFRNHR

Vigenere cipher analysis

It’s stronger than a Caesar Cipher
- ‘e’ can be encrypted multiple ways
The weakness is the repeating key
- If you guess the length of the key (or try all possible lengths), then you can crack it
- Let’s say the key is length 5 (a guess, perhaps)
- Then you simply do 5 interwoven Caesar Cipher cracks
What if the key is as long as the message?
Reference

One-time pad (OTP)

A substitution cipher
Take a random string that is as long as the plain text you want encrypt
- Use modular arithmetic (or XOR, or Vigenere) to determine the encrypted version
- Plain text: helloworld
- One-time pad: zdxwhtsvtv
- Encrypted: hijiwqhnfz
Reference

One-time pad (OTP) analysis

Pros
- Proven to be perfectly secure if:
  - the pad is truly random
  - the pad is only used once
  - the pad is kept secret
- This, it is the ONLY cryptosystem with perfect secrecy
- It can be performed by hand

One-time pad (OTP) analysis

Cons:
- Good for short messages; it’s hard to transport large pads (i.e. network communication)
- Does not provide message authentication
- How do you get the pad to the recipient?

Re-using a one-time pad

Use an OTP:	⊕ =
Re-use the same OTP:	⊕ =
Extract the images:	⊕ =

This example from StackExchange

Route cipher

A transposition cipher
- The plain text is written in a grid
- The secret is the direction to read the cipher text
Plain text: ‘we are discovered flee at once’
Cipher progression:

R E D F L E E A W 
E J X E C N O T E 
V O C S I D E R A

Key: “spiral inwards, clockwise, starting from the top right”
Cipher text: REDFLEEAWEJXECNOTEVOCSIDERA
Reference

Rail fence cipher

A transposition cipher
- The plain text is written up and down on successive ‘rails’ of a fence
- The encrypted text is then read off in rows
Plain text: ‘we are discovered flee at once’
Cipher progression:

W . . . E . . . C . . . R . . . L . . . T . . . E
. E . R . D . S . O . E . E . F . E . A . O . C .
. . A . . . I . . . V . . . D . . . E . . . N . .

Cipher text: WECRL TEERD SOEEF EAOCA IVDEN
Reference

WW2 Navajo Code Talkers

Used during the American strategy of island-hopping in the Pacific during WW2
Native Navajo speakers (which were only in the US!) were used to send messages back and forth over radio frequencies that could be spied on
The ‘encryption’ or cipher was the language
- There were no written documents or dictionaries in existence
- Other than Navajo Native Americans (all in the US, obviously), there were only 30 or so people who were fluent

WW2 Navajo Code Talkers

But there was a code as well
- Navajo words were translated into their English equivalents
- The first letter of each English translated word was combined to form the message
- If you didn’t know this, it would be a series of unconnected Navajo words
It has been stated that the US would not have won the Battle of Iwo Jima without the Navajo code talkers
References 1 and 2

Rotor machines

It performs a simple substitution of letters
After encrypting each letter, the rotors advance positions
Thus, they implement a poly-alphabetic substitution cipher
- Similar to the Vigenere cipher
Reference

Rotor machines

Enigma machine

Most famous rotor machine
Used by many governments in WW2, especially Nazi Germany
The Allies were able to decrypt Nazi messages
- But not through crypto-graphically cracking the code!
This is estimated to have shortened the war in the European theater by 2 years
Reference

Enigma machine

Private key “symmetric” ciphers

Data Encryption Standard (DES)

Adopted in 1976, it’s a private-key encryption/decryption block cipher
Briefly, it does a lot of (invertible) bit-shifting in rounds to encrypt/decrypt a message
How to crack?
- It is susceptible to brute force attacks ($2^{56} = 7 * 10^{16}$ keys)
Solution: use DES three times => “Triple DES”
- Use a 56*3 = 168 bit key, and encrypt the message three times, once with each key

Cracking Triple DES encryption

Brute-force attacks:
- $2^{168}$ keys, but due to various mathematical properties, this ends up being $2^{112}$ different keys
“The best attack known on 3-key TDES requires around $2^{32}$ known plaintexts, $2^{113}$ steps, $2^{90}$ single DES encryptions, and $2^{88}$ memory”
NIST (National Institute of Standards and Technology) considers it secure through 2030

DES conspiracy theories

NSA was involved with DES’ creation
- They convinced IBM to lower the key length from 128 to 64, and then to 56
- And kept many of the details secret
- Many well-respected people criticized the NSA for “improper interference” with the algorithm
In 1977, Diffie and Hellman (major names in cryptography) proposed a $20 million machine that could crack a DES message in a single day
It’s known that the NSA had the budget for such a machine. But did they build it?

Advanced Encryption Standard (AES)

The successor to DES
Has three possible key lengths: 128, 192, and 256
NSA approved this standard, and kept the process open
Like DES, it’s a series of (invertible) bit-shifting in rounds to encrypt/decrypt a message
Many worry about the security of the standard
- … that somebody may figure a way to crack it mathematically, in particular
Reference

AES Overview

Determine number of rounds, $r$:
- 10, 12, or 14 rounds for 128-bit, 192-bit, and 256-bit keys
KeyExpansion: derive round keys from Key Round Schedule
Round 1: AddRoundKey: XOR with round key
Rounds 2 through $r-1$:
- SubBytes, ShiftRows, MixColumns, AddRoundKey
Final round $r$:
- SubBytes, ShiftRows, AddRoundKey

Key Round Schedule

Let:
- $N$: key length in 32-bit words (4, 6, or 8)
- $K_0, K_1, \ldots K_{N-1}$: 32-bit words of the key
- RotWord is a left rotation by 1
- SubWord is a lookup
- $R_{con}$ is a fixed round constant
Then repeat the image many times
It’s fixed for that one key, so only has to be computed once

AES: SubBytes step

Input is mapped to its mult. inverse in a finite field
Bytes are replaced based on a fixed substitution table
- Fixed for all of AES
Called the Rijndael S-box

AES: ShiftRows step

Rows are shifted cyclically to the left
This provides diffusion

AES: MixColumns step

The values are transformed according to the following matrix operation
This also provides diffusion

$\begin{bmatrix} b_{0,j} \\\ b_{1,j} \\\ b_{2,j} \\\ b_{3,j} \end{bmatrix} = \begin{bmatrix} 2&3&1&1 \\\ 1&2&3&1 \\\ 1&1&2&3 \\\ 3&1&1&2 \end{bmatrix} \begin{bmatrix} a_{0,j} \\\ a_{1,j} \\\ a_{2,j} \\\ a_{3,j} \end{bmatrix} \text{ for }0 \le j \le 3$

AES: AddRoundKey step

Derive a subkey from the main key via the AES key schedule
Subkey is then XOR’ed with the state

AES Overview

Determine number of rounds, $r$:
- 10, 12, or 14 rounds for 128-bit, 192-bit, and 256-bit keys
KeyExpansion: derive round keys from the AES Key Round Schedule
Round 1: AddRoundKey: XOR with round key
Rounds 2 through $r-1$:
- SubBytes, ShiftRows, MixColumns, AddRoundKey
Final round $r$:
- SubBytes, ShiftRows, AddRoundKey

Number Theory

Is that number prime?

Use the Fermat primality test
Given:
$n$: the number to test for primality
$k$: the number of times to test (the certainty)
The algorithm is:

repeat k times: 
    pick a random number in the range [1, n-1]
    if a^{n-1} mod n != 1 then return composite
return probably prime

Is that number prime?

The algorithm is:

repeat k times: 
    pick a random number in the range [1, n-1]
    if a^{n-1} mod n != 1 then return composite
return probably prime

Let $n = 105$
- Iteration 1: $a = 92: 92^{104} \text{ mod }105 = 1$
- Iteration 2: $a = 84: 84^{104} \text{ mod }105 = 21$
- Therefore, 105 is composite

Is that number prime?

The algorithm is:

repeat k times: 
    pick a random number in the range [1, n-1]
    if a^{n-1} mod n != 1 then return composite
return probably prime

Let $n = 101$
- Iteration 1: $a = 55: 55^{100} \text{ mod } 101 = 1$
- Iteration 2: $a = 60: 60^{100} \text{ mod } 101 = 1$
- Iteration 3: $a = 14: 14^{100} \text{ mod } 101 = 1$
- Iteration 4: $a = 73: 73^{100} \text{ mod } 101 = 1$
- At this point, 101 has a $(1/2)^4 = 1/16$ chance of still being composite

More on the Fermat primality test

Each iteration halves the probability that the number is a composite
- Probability = $(1/2)^k$
- If $k = 100$, the probability it’s a composite is $(1/2)^{100} = 1\text{ in }1.2 * 10^{30}$ that the number is composite
  - Greater chance of having a hardware error!
- Thus, $k = 100$ is a good value

Google’s recruitment campaign

How to compute $a^e\text{ mod }n$ ?

We can’t compute $a^e$ directly
- If they are 1200 digit numbers, then $a^e$ will be well over a million digits
- Regardless of the memory usage, that will take quite some time to compute
Answer: we compute it in steps, and take the mod after each step
- This keeps the overall value down (below $n$) since we are mod’ing each time

Compute $a^{1652} \text{ mod } n$

Note $1652 = 2^{10} + 2^9 + 2^6 + 2^5 + 2^4 + 2^2$
Parts:
- Compute $a^2 \text{ mod } n$, which is one multiplication ($a \cdot a$) and one modulus
- Compute $a^4 \text{ mod } n$, which is a mult (of $a^2 \cdot a^2$) and a mod
- Compute $a^8 \text{ mod } n$, which is a mult and a mod
- …
- Compute $a^{1024} \text{ mod } n$, which is a mult (of $a^{512} \cdot a^{512}$) and a mod

Compute $a^{1652} \text{ mod } n$

Then $a^{1652} = a^{1024} \cdot a^{512} \cdot a^{64} \cdot a^{32} \cdot a^{16} \cdot a^{4}$
This will require:
- 10 multiplications and 10 mods to list of the powers
- Up to 10 more to compute the final product
The result is $\log_2(e)$ operations where $e$ is the exponent
- With 1200 digit numbers, that’s about 4,000 steps
- Memory usage is (relatively) minimal, as we keep mod’ing each time

Running the Fermat primality test

We can now compute $a^e \text{ mod } n$
To run the test, we repeat:
- Pick a random (odd) number of the correct bit size
- Is it prime as per the Fermat primality test?
- If prime, break
- If not prime, then continue
We will see Java and Python code to do all this in a moment…

Primarily test conclusions

If it says “composite” just once, it’s definitely composite
Otherwise, it just says “probably prime”
Takes polynomial time (it’s “easy” to compute)
We use $k=100$, as a hardware error is more likely beyond that
The computation involved is $a^{n-1}\text{ mod }n \neq 1$
- For 1200 digit numbers (what is used in practice), this is a significant computation!
- We will use existing libraries to compute this

Bit size

A 100 bit integer is about 30 decimal digits
- You divide the number of bits by $\log_2(x) / \log_d (x) \approx 3.32$
- Here, $\log_d(x)$ is log base 10
Thus, a 32 bit integer is about 9.6 digits (4 billion is just over 9 digits)
A 2048-bit number is 616 decimal digits
- A typical length for an RSA key
A 4096-bit number is 1,233 decimal digits
- A very secure RSA key
These are the sizes of numbers we are dealing with…

The prime number theorem

The number of prime numbers less than $x$ is approximately $x/\text{ln}(x)$ (reference)
- Rephrased: the chance of a number $x$ being a prime number is roughly $1 / \text{ln}(x)$
Consider 200 digit prime numbers
- $\text{ln} (10^{200}) \approx 460$
- The chance of a random 200 digit number being prime is thus 1/460
- For only odd numbers, the chance is 2/460 = 1/230
- For a 2048 bit odd number (616 decimal digits) it’s about 1/710

RSA

Private key cryptography

The function and/or key to encrypt/decrypt is a secret
(Hopefully) only known to the sender and recipient
The same key encrypts and decrypts
How do you get the key to the recipient?

Public key cryptography

Everybody has a key that encrypts and a separate key that decrypts
They are not interchangable!
The encryption key is made public
The decryption key is kept private

Public key cryptography goals

Key generation should be relatively easy
Encryption should be easy (polynomial time)
Decryption should be easy (polynomial time)
- With the right key!
Cracking should be very hard (exponential time)

RSA

Stands for the inventors: Ron Rivest, Adi Shamir and Len Adleman
Three parts:
- Key generation
- Encrypting a message
- Decrypting a message

Key generation steps

Choose two random large prime numbers $p$ and $q$ such that $p \neq q$, and then compute $n = p*q$
Choose an integer $1 < e < n$ which is relatively prime to $(p-1)(q-1)$
Compute $d$ such that:
- $d * e \equiv 1 (mod (p-1)(q-1))$
- Rephrased: $d*e \text{ mod }(p-1)(q-1) = 1$
Destroy all records of $p$ and $q$

Key generation, step 1

Choose two random large prime numbers $p \neq q$
- In reality, 2048 bit numbers are recommended
  - That’s about 617 decimal digits
- Chance of a random odd 2048 bit number being prime is about 1/710
  - We can compute if a number is prime relatively quickly via the Fermat primality test
We choose $p = 107$ and $q = 97$
Compute $n = p*q$
- $n = 10379$

Key generation, step 1

Java code to find a big prime number:

BigInteger prime = new BigInteger
          (numBits, certainty, random);

Yes, it’s that easy
That constructor runs the Fermat primality theorem
- And handles the $a^e \text{ mod } n$ computations necessary
Python code: see two slides down

Key generation, step 1

Full Java class to find a big prime number:

import java.math.*;
import java.util.*;
public class BigPrime {
    static int numDigits = 617;
    static int certainty = 100;
    static final double LOG_2 = Math.log(10)/Math.log(2);
    static int numBits = (int) (numDigits * LOG_2);
    public static void main (String args[]) {
        Random random = new Random();
        BigInteger prime = new BigInteger (numBits, 
                             certainty, random);
        System.out.println (prime);
    }
}

Key generation, step 1

Full Python code to find a big prime number:

def fermat_test(n, k):
    # adapted from https://gist.github.com/Ayrx/5884802
    for i in range(k):
      a = random.randint(1, n-1)
      if pow(a, n-1, n) != 1:
        return False
    return True

Usage:

>>> import random
>>> # define fermat_test() as above
>>> fermat_test(101,20)
True
>>> fermat_test(10101,20)
False
>>>

Key generation, step 1

How long does this take?
- On a modern (3.4 Ghz) machine, the Java version took between 1/2 and 3 seconds
  - Different runs require a different number of random number generations
- And this is Java – it would be faster in C or C++

Key generation, step 1

Practical considerations
- $p$ and $q$ should not be too close together
- $(p-1)$ and $(q-1)$ should not have small prime factors
Use a good random number generator

Key generation, step 2

Choose an integer $1 < e < n$ which is relatively prime to $(p-1)(q-1)$
There are algorithms to do this efficiently…
- … but we aren’t going to go over them in this course
One easy way to do this: make $e$ be a prime number
- It only has to be relatively prime to $(p-1)(q-1)$, but it can be fully prime
$e$ should be a bit smaller than $n$ (maybe by a factor of 10 or 100 or so)

Key generation, step 2

Recall that $p = 107$ and $q = 97$
- $(p-1)(q-1) = 106 \ast 96 = 10176$
- $10176 = 2^6 \ast 3 \ast 53$
We choose $e = 85$
- $85 = 5*17$
- $\text{gcd}(85, 10176) = 1$
Thus, 85 and 10176 are relatively prime
- Even though 85 is compisite

Key generation, step 3

Compute d such that:
- $d \ast e \equiv 1 (\text{mod } (p-1)(q-1))$
- Rephrased: $d \ast e \text{ mod } (p-1)(q-1) = 1$
There are algorithms to do this efficiently…
- … but we aren’t going to go over them
We determine $d = 4669$
- $4669 \ast 85 \text{ mod } 10176 = 1$

Key generation, step 3

Java code to find d:

import java.math.*;
public class FindD {
    public static void main (String args[]) {
        BigInteger pq = new BigInteger("10176");
        BigInteger e = new BigInteger ("85");
        System.out.println (e.modInverse(pq));
    }
}

Result: 4669
Python code to find d:

>>> pq=10176
>>> e=85
>>> pow(e,-1,pq)
4669
>>>

Key generation, step 4

Destroy all records of $p$ and $q$
- If we know $p$ and $q$, then we can compute the private encryption key from the public decryption key via:
- $d * e \equiv 1 (\text{mod }(p-1)(q-1))$

The keys

We have $n = p*q = 10379$, $e = 85$, and $d = 4669$
The public key is $(n,e) = (10379, 85)$
The private key is $(n,d) = (10379, 4669)$
Thus, $n$ is not private; only $d$ is private
In reality, $p$ and $q$ are 616 (or so) digit numbers
- As that is 2048 bits
- Thus $n$ is a 1200 (or so) digit number
- $d$ and $e$ are about 1,199 (or so) digit numbers

Encrypting messages

To encode a message:
1. Encode the message $m$ into a number
2. Split the number into smaller numbers $m < n$
3. Use the formula $c = m^e \text{ mod }n$
  - $c$ is the ciphertext, and $m$ is the message
Java code to do the last step:
- Where the object $m$ is the BigInteger to encrypt
```
m.modPow (e, n)
```
Python code to do the last step:

pow(m,e,n)

Don’t use m ** e % n in Python, as it’s too slow

Encrypting RSA messages

Formula is $c = m^e\text{ mod }n$ RSA license plate

Encrypting messages example

Encode the message into a number
- String is “Go Cavaliers!!”
- Modified ASCII codes:
- 41 81 02 37 67 88 67 78 75 71 84 85 03 03
Split the number into numbers $< n$
- Recall that $n = 10379$
- 4181 0237 6788 6778 7571 8485 0303

About the modified ASCII codes

I modify the ASCII codes for this example
By subracting 30 from each value
This is just so this example in the slides can use smaller values for $p$ and $q$
You should NOT be using modified ASCII codes in the RSA homework!

Encrypting messages example

Use the formula $c = m^e \text{ mod }n$
- $4181^{85}\text{ mod }10379 = 4501$
- $0237^{85}\text{ mod }10379 = 2867$
- $6788^{85}\text{ mod }10379 = 4894$
- Etc…
Encrypted message:
- 4501 2867 4894 0361 3630 4496 6720

Decrypting messages

Use the formula $m = c^d\text{ mod }n$ on each number
Split the number into individual ASCII character numbers
Decode the message into a string

Decrypting messages example

Encrypted message:
- 4501 2867 4894 0361 3630 4496 6720
Use the formula $m = c^d\text{ mod }n$ on each number
- $4501^{4669}\text{ mod }10379 = 4181$
- $2867^{4669}\text{ mod }10379 = 0237$
- $4894^{4669}\text{ mod }10379 = 6788$
- Etc…

Decrypting messages example

Split the numbers into individual characters
- 41 81 02 37 67 88 67 78 75 71 84 85 03 03
Decode the message into a string
- Modified ASCII codes:
  - 41 81 02 37 67 88 67 78 75 71 84 85 03 03
  - Retrieved String is “Go Cavaliers!!”

modPow computation

How to compute $c = m^e\text{ mod }n$ or $m = c^d\text{ mod }n$?
- Example: $4501^{4669}\text{ mod }10379 = 4181$
Computation means:
- Java: use the BigInteger.modPow() method
- Perl: use the bmodpow() function in the BigInt library
- C++: Use the bigint class (http://sourceforge.net/projects/cpp-bigint/)
- Python: use the 3-parameter version of pow()
- Etc…

Why does this work?

The values of $d=4669$ and $e=85$ are the inverse of each other for exponentiation within $n=10379$
- $(x^e)^d \text{ mod } n == x$

$ python3
>>> e=85
>>> d=4669
>>> n=10379
>>> (1024 ** d) ** e % n
1024
>>> (1234 ** d) ** e % n
1234
>>> (3710 ** d) ** e % n
3710
>>> (9999 ** d) ** e % n
9999
>>> exit()
$

Cracking a message

In order to decrypt a m, we must compute $m = c^d \text{ mod }n$
- $n$ is known (part of the public key)
- $c$ is known (the ciphertext)
- $e$ is known (the encryption key)

Cracking a message

Thus, we must compute $d$ with no other information
- Recall: $n = p \ast q$
- Recall: choose an integer $1 < e < n$ which is relatively prime to $(p-1)(q-1)$
- Recall: Compute $d$ such that: $d \ast e\text{ mod }(p-1)(q-1) = 1$
Thus, given $n$ and $e$, we have to compute $d$

Cracking a message

Thus, we must factor the composite $n$ into its component primes
- There is no efficient way to do this!
- We can, very easily, tell that $n$ is composite, but we can’t tell what its factors are
Once $n$ is factored into $p$ and $q$, we compute $d$ as above
- Then we can decrypt $c$ to obtain $m$

Cracking a message example

In order to decrypt a message, we must compute $m = c^d\text{ mod }n$
- $n = 10379$, $e = 85$, and $c$ is the ciphertext
In order to determine $d$, we need to factor $n$
- $d \ast e\text{ mod }(p-1)(q-1) = 1$
- We factor $n$ into $p$ and $q$: 97 and 107
- This would not have been feasible with two large prime factors!!!
- $d \ast 85 (\text{mod }(96)(106)) = 1$
We then compute d as above, and crack the message

Why RSA is considered secure

RSA security is based on two principles:
- First: factoring large composites into their prime factors is hard
- In 2005, a 193-digit number was factored using 12.5 CPU years on a 2.2 GHz Operon CPU (actually 5 months on 30 CPUs)
- The best algorithm for factoring large numbers (general number field sieve) is $O(e^n)$

Why RSA is considered secure

RSA security is based on two principles:
- Second: the “RSA problem”: finding the $e^{th}$ roots modulo a composite number $N$ is hard
- Specifically, given $c = m^e\text{ mod } n$, and knowing $c$, $e$, and $n$, finding $p$ is hard
- Considered as hard as integer factorization

Current factoring state of the art

“As of the end of 2007, thanks to the constant decline in memory prices, the ready availability of multi-core 64-bit computers, and the availability of [efficient factoring software], special-form numbers of up to 750 bits and general-form numbers of up to about 520 bits can be factored […]. These bounds would increase to about 900 and 600 [on a] few dozen PCs”
- We used 2048 bit (617 decimal digit) numbers!
- http://en.wikipedia.org/wiki/Integer_factorization_records

Signing a message

Recall that we computed:
- $d*e\text{ mod }(p-1)(q-1) = 1$
Note that $d$ and $e$ are interchangeable!
- You can use either for the encryption key
You can encrypt with either key!
- Thus, you must use the other key to decrypt

Signing a message

To “sign” a message:
1. Write a message, and determine the SHA-256 (or similar) hash
2. Encrypt the hash with your private (encryption) key
3. Anybody can verify that you created the message because ONLY the public (encryption) key can decrypt the hash
4. The hash is then verified against the message

Signing a message

You are encrypting the HASH of the message
- And doing so with your PRIVATE key
The message itself is not being encrypted at all
Anybody can decrypt the encrypted hash by using your public key
- And verify that it matches, as they can compute the hash themselves

Signing a message: detail

Write out a plaintext message $m$
Take the SHA-256 (or similar) hash of the message $m$ to get hash value $h$
Encrypt $h$ with your private key $(n,d)$ to get $c$
- This is your private key that is being used for encryption here
The message you send is $x = m \cdot c$
- That’s concatenation

Checking a message signature: detail

You receive message $x = m \cdot c$ from somebody with public key $(n,e)$
You separate $x$ into it’s constituent parts $m$ and $c$
You decrypt $c$ using public key $(n,e)$ to get $h_1$
- That’s the public key being used for decryption here
You take the SHA-256 (or similar) hash of $m$ to get $h_2$
If $h_1$ and $h_2$ match, then it was signed by the person with the private key that matches public key $(n,e)$

PGP and GnuPG

Two applications which implement the RSA algorithm
PGP was written in 1991 by Phil Zimmerman
- The US government didn’t like PGP…
Gnu Privacy Guard (GnuPG) is open-source (thus it’s free) implementation of PGP, written in 1999
Both follow the OpenPGP Message Format
- Specified in RFC 4880

The US gov’t and war munitions

war munition shirt 1 war munition shirt 2

RSA vulnerabilities

If $e$ is small, and $m$ is small (such that $m^e < n$), then the ciphertext can be easily decrypted
If multiple receivers share the same $e$, but different $p$, $q$, and $n$, then the same clear text message encrypted for the multiple receivers can be cracked via the Chinese remainder thoerem
RSA is vulnerable to chosen plaintext attacks (where you encrypt likely plain texts and compare it to the cipher text)
Etc.

Solution

Pad the message to make it longer
- And add random bits in the padding to prevent multiple encryptions of the same plain text from being the same cipher text
There are standards for doing this (PKCS#1)

How to “crack” RSA

Factoring $n$ is not feasible
Thus, “cracking” RSA is done by other means
Intercepting the private key
- “Hacking” into the computer, stealing the computer, etc.
- Man-in-the-middle attack (next few slides)
- Etc.

Security

Actual actual reality: nobody cares about his secrets. (Also, I would be hard-pressed to find that wrench for $5.)

xkcd # 538

“Normal” RSA communication

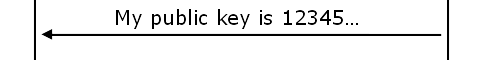
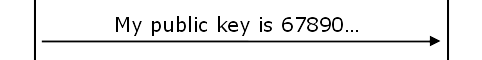
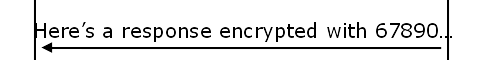
SSH display to get a key

Man-in-the-middle attack

An attacker (“Mallory”) intercepts the communications between two participants, and relays messages between them
- Perhaps Mallory has access to a router that the messages pass through
- Obviously, the participants (“Alice” and “Bob”) are unaware that Mallory is relaying the messages
Specifically, we assume that Mallory can MODIFY the messages being sent
- Not just listen to them

MITM RSA communication

SSH display with a possible MITM

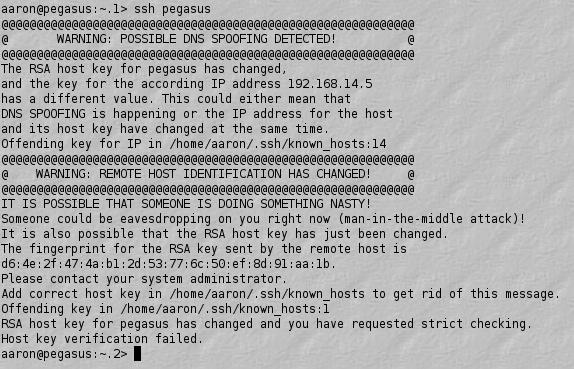
How to prevent MITM attacks

You need a way to ensure that the key you get is the correct key
This gave rise to key stores
- Store in the sense of storage, not selling things
A key store’s public key was well known and widely published
When you create a key, you upload it to the key store
- Somebody else would get your key from the key store
Still possible for me to upload a key and claim it’s yours, though…

Other public key encryption methods

The goals are the same as RSA
- There must be two keys, which are paired
- Encryption and decryption (with the key!) should be “easy” (i.e. polynomial time)
- Cracking the message should be “hard” (i.e. exponential time)
Other ideas:
- Discrete logarithms (next slide)
- Elliptic curves (next->next slide)

Discrete logarithms

Consider a mathematical group, or a congruence class, such as $Z_{12}$
- This is the same as a clock: add numbers, and mod the result by 12
Exponentiation: $3^4 = 81$
- But in the $Z_{17}$, 81 is really 13 as $81\text{ mod }17 = 13$)
- Thus $3^4 = 13$ in $Z_{17}$
- Or ${\log}_3 13 = 4$
Exponentiation is “easy”, but finding a logarithm is “hard”
Reference

Elliptic curves

A curve of the form $y^2=x^3+a\cdot x+b$

History

1976: Whitfield Diffie and Martin Hellman publish “New Directions in Cryptography”, which proposes a public-key (i.e. asymmetric) system
1978: RSA is invented by Rivest, Shamir, and Adleman
1997: Whoops! It turns out Diffie-Hellman and RSA were invented (independently) a bit earlier
- Diffie-Hellman by a British intelligence service (GCHQ) in ’74
- RSA, also by the same British intelligence service, in 1975

Quantum computers

A quantum computer could (in principle) factor $n$ in reasonable time ($O(b^3)$, where $b$ is the number of bits)
- This would make RSA obsolete!
- Shown (in principle) by Peter Shor in 1993
- You would need a new (quantum) encryption algorithm to encrypt your messages
This is like saying, “in principle, you could program a computer to correctly predict the weather”
I bet the NSA is working on such a computer, also
In 2022, a 48-bit number was factored using a quantum computer (source: wikipedia)
- Modern RSA has $n$ with 4,096 or 8,192 bits

Quantum computing factorization

In 2012, UCSB built a quantum computer that can factor 15 into 3*5 with 48% accuracy
- Yes, really
- (Okay, I realize that it was a big advancement, but come on now…)
- And it cost a lot of money…
reference

Latest quantum computing stats

April 2012: 143 factored into 13*11
April 2016: factored 200,099 into 401*499
reference

Should we be worried?

Probably not just yet
It will likely be a while before quantum computers can be used to factor numbers used in modern encryption
And, at that point, we’ll just use quantum encryption
- See here for more details…

Randomness

Random Number

xkcd # 221

Computers and randomness

A computer, by definition, produces the same output for the same input
So how, then, can it produce truly random numbers?
The answer: it can’t
- We instead generate pseudo-random numbers
Pseudorandomness: “A pseudorandom process is a process that appears to be random but is not”
- That’s all a computer can really generate

Necessity of randomness

Much of encryption depends on randomness
If you could “guess” the random number sequence, then you could figure out the one-time pad
- … or the generated ssh keys, or the RSA keys…
So we need really good random numbers
Formally, we need a cryptographically secure pseudorandom number generator
- Formal definition shortly, but basically, it produces pseudo-random numbers that appear truly random

Typical generation method

The linear congruential generator (LCG)
$X_{n+1}=(a*X_n+c) \text{ mod } m$
- $m$ is the modulus, and must be positive
- $a$ is the multiplier: $0 < a < m$
- $c$ is the increment: $0 < c < m$
- $X_0$ is the seed value
This will cycle through all values less than $m$ iff:
- $m$ and $c$ are relatively prime (i.e, $\gcd(m,c)=1$)
- $a-1$ is divisible by all prime factors of $m$
- $a-1$ is divisible by 4 if $m$ is divisible by 4

Typical method: example

Let $m=9$, $a=4$, $c=7$
We’ll arbitrarily decide to start the sequence at 1
- Thus, $X_0=1$
Will this cycle through all values less than $m$?
- $m$ and $c$ are relatively prime: yes, as $\gcd(9,7)=1$
- $a-1$ is divisible by all prime factors of $m$: yes, the factors of 9 (3, 3) also divide 3 (which is $a-1$)
- $a-1$ is divisible by 4 if $m$ is divisible by 4: not applicable, as 3 (which is $a-1$) is not divisible by 4

Typical method: example

Let $m=9$, $a=4$, $c=7$
This will cycle through all the values, as shown on the last slide
$X_{n+1}=(a*X_n+c) \text{ mod } m$
- $X_0 = 1$
- $X_1 = (4*1+7) \text{ mod } 9 = 2$
- $X_2 = (4*2+7) \text{ mod } 9 = 6$
- $X_2 = (4*6+7) \text{ mod } 9 = 4$
- $X_3 = (4*4+7) \text{ mod } 9 = 5$
- Rest of the sequence: 0, 7, 8, 3, and then back to 1

Typical method: example

The linear congruential generator (LCG) sequence with $m=9$, $a=4$, $c=7$:
- 1, 2, 6, 4, 5, 0, 7, 8, 3, and then back to 1
But where to start in the sequence?
- We could start anywhere therein
Where we start is called the seed
Different seed values just start at a different spot in the cycle of random numbers

LCG parameters in use

libc uses $a=1103515245$, $c=12345$, and $m=2^{31}$
- This is what is called by rand() in C and C++; setting the seed is done by srand()
- This will cycle through 2 billion ($2^{31}$) values before repeating
It will cycle through all the values, as per the three properties defined earlier
With a seed of 1, the initial sequence is:
- 1, 1103527590, 377401575, 662824084, 1147902781, 2035015474, 368800899, …

LCG parameters in use

RANDU used $a=65539$, $c=0$, and $m=2^{31}$
- Used from the 1960’s, it created a very easy to calculate sequence on old hardware
- See Why RANDU is a bad random number generator
It does NOT cycle through all possible numbers
- $\gcd(2^{31},0)\neq 1$, as $\gcd(a,0)=a$
- $a-1=65538$ is not divisible by 4 whereas $m=2^{31}$ is
With a seed of 1, the initial sequence is:
- 1, 65539, 393225, 1769499, 7077969, 26542323, …
- All odd numbers!

LCG parameters in use

See here for more possibilities

What seed to use?

If you use the same seed, you will always get the same random sequence
Many people use time(NULL) in C/C++
- This is the current number of seconds since January 1st, 1970
- Which is how UNIX systems keep track of time
But if you run the program twice in the same second, it will use the same sequence!
That being said, this is probably sufficient for non-cryptographic purposes
- You could use the current time in milliseconds…

More randomness

There are many and better pseudo-random number generators
Those that are computationally indistinguishable from true random numbers are considered suitable for cryptography
- These is what defines a cryptographically secure pseudorandom number generator
But how to get the initial seed?
- Especially when computers produce the same output on the same input?

More randomness

We need a randomness extractor:

“a function, which being applied to output from a weakly random entropy source, together with a short, uniformly random seed, generates a highly random output that appears independent from the source and uniformly distributed”

More randomness

So how to get that “weakly random entropy source”?
You could use other input values such as:
- The 10th and 11th bit of the floating point value read in from the CPU temperature sensor
- Or the hash of that entire temperature value (use a good hash, as described later in this slide set)
- Or any other sensor that the computer has available
- Or many other methods

Cloudflare uses a wall of lava lamps (source)

Determining randomness

To tell if a number sequence is truly (pseudo-) random, you run randomness tests on it
Examples:
- Run it a bagillion times and see if the distributions of the numbers is uniform across the range
- See if the numbers follow a normal distribution (when run through the correct formulas)
- Interpret the numbers as 5 card stud poker hands, and see if the distrubtion of hands is the expected distribution
- And many others…

Debian OpenSSL predictability

A bit of background first…
Open source software is maintained by certain individuals
- Here called the “upstream developers”
Different Linux distrubtions will package them for easy installation
- Example: sudo apt-get install openssl
- Volunteers, called “package maintainers” do this work
  - They are typically not the upstream developers

Debian OpenSSL predictability

Package maintainers do the following:
- Compile the (upstream) source code for various hardware platforms
- Change the configuration to match the system default (location of config files, etc.)
- Specifying the necessary dependent libraries / packages
- Putting all this together into an installable package, and uploading that to the distribution’s servers

Debian OpenSSL predictability

In 2007 or 2008, the package maintainer for OpenSSL (the primary cryptographic library) noticed a series of warnings the compiler generated, and tracked them down to a given line in the code
Not being familiar with the code, he asked the upstream developer if that line could be removed
The upstream developer said “yes”
The line was removed, and the package distributed

Debian OpenSSL predictability

But that line is what added the randomness!
Without it, there were only 65k possible SSH keys that could be generated!
- Any computer could generate all of them in less than a day
Once patched, everybody had to regenerate their ssh keys…
Read more here

Security Holes

True story: I had to try several times to upload this comic because my ssh key was blacklisted.

xkcd # 424

Dependency

Someday ImageMagick will finally break for good and we'll have a long period of scrambling as we try to reassemble civilization from the rubble.

xkcd # 2347

Hashing

Ensuring the download is correct…

What if we don’t want to encrypt the data?
- So anybody can download it: patches, open source code, etc.
- But we want to be sure to allow those people to verify that they downloaded the correct file
  - And that they didn’t have any download errors
Solution: provide a hash code of the file

Hashing properties

Hash goals:
- Changing even a single bit has a dramatic effect on the hash code
Pigeon hole principle:
- If we use a 128-bit hash, that yields $2^{128} \approx 3.4 * 10^{38}$ possible values
- If we have files that are 129+ bits, then there will be more possible files than there are hashes
- Thus, multiple files will provide the same hash
- This will hold for all hashes, as long as the hash code is of a finite length

Hash vulnerabilities

For a hash function to be really vulnerable, we want to be able to take an arbitrary text and make it match the desired hash code
- Sender sends: “deposit $1 million into account 12345” with hash “abcdefg”
- You intercept and send a new message: “deposit $1 million into account 67890; (fl_0” with hash “abcdefg”
  - The trailing “; (fl_0” allowed the different document to match the same hash

Hash vulnerabilities

Being able to create two “random” files that match the same hash indicates a weakness, but is not yet a vulnerability

Hashes are one-way!

Consider the following two files:

(from here, as it may not render properly on the slides)

1i=\/ʵF~@X>U4 䈃%qAZQ%ɟ7<[؂>1V4[m6Sⴇ9cH͠3BW~Tp
Ƙ!e+o*p

1i=\/ʵF~@X>U4    䈃%AZQ%ɟr7<[؂>1V4[m6S49cH͠3BW~Tp(
Ƙ!eo*p

The both have the same MD5 hash of 79054025255fb1a26e4bc422aef54eb4
So given the MD5 hash, how do we know which one it came from?

Pigeonhole principle

An MD5 hash is 128 bits; SHA hashes go up to 512 bits
There are more files possibilites of 129 bits (or 513 bits) than there are possible hashes
Thus, as per the pigeonhole principle, there will be multiple inputs for a given hash
So how do you know how to go back from a hash?
- Answer: you don’t

Collision resistant hashes

A collision resistant hash means that it is “hard” to find two inputs that hash to the same value
- Harder than, say, brute force
- If there is any way easier than brute force, that’s bad

Collision resistant hashes

Due to the birthday paradox, one will typically have to brute force $2^{n/2}$ attempted values before a collision is found
- For MD5 (128 bits): $2^{128/2} = 2^{64} = 1.84 * 10^{19}$ attempts
  - Computing 1 million a second takes $5.85 * 10^{11}$ years
  - But a better attack can achieve this in under a minute
  - (MD5 is not collision resistant, as described later)

Collision resistant hashes

For SHA-256 (256 bits): $2^{256/2} = 2^{128} = 3.40 * 10^{38}$ attempts
- Computing 1 million a second takes $1.08 * 10^{31}$ years
reference

CRC32: Cyclic Redundancy Check

The hash value is a 32-bit integer
- There are variants of other bits: 16, 64, etc.
Is used for downloading files (via modem, download program, etc.) – i.e. as a checksum
- It works great for this purpose
With the (simple) math behind the checksum, and “only” 4 billion possibilities, one can target a specific CRC 32 hash value
- This is a homework problem in the hashing homework

MD5: Message Digest 5

Produces a 128-bit value ($3.4 * 10^{38}$ possible values)
- Expressed as a 32-digit hex number
Was the most widely used algorithm
Designed in 1991 when research indicated its predecessor (MD4) was insecure
Printed in hex:

$ md5sum message1.txt 
afe68f753a65f773a591bcf6f9ce3c63  message1.txt

MD5: Message Digest 5

Still widely used for file downloading
- CERT: “should be considered cryptographically broken and unsuitable for further use”
A number of collisions have been found:
- 1996: “first” collisions found
- 2005: public keys (with associated private keys) could be constructed that have the same MD5 hash
- 2008: researchers faked SSL certificate validity by creating keys with desired MD5 hashes
You can create two programs with the same MD5 hash

SHA-0 and SHA-1

Designed by the NSA
- After the DES debacle, it’s become an open standard
- Published by NIST (National Institute of Standards and Technology)
160 bit hash
SHA-0 (1993): had a flaw, was quickly corrected
- The flaw introduced an unintended weakness
SHA-1 (1995): fixed that flaw, was very widely used for security applications
- But typically not for downloading files

SHA-0 and SHA-1

In 2005, security flaws were discovered in SHA-1
- A vulnerability has not been shown, however
- reference

SHA-2

Designed in 2001 to address the flaw discovered in SHA-1
- There are 4 variants, depending on the length of key desired: SHA-224, SHA-256, SHA-384, SHA-512
SHA-2 is mathematically similar (but not identical!) to SHA-1 (source code)
- So if there are vulnerabilities in SHA-1, do they exist in SHA-2?
- Nobody knows, but this lead to the development of SHA-3
Most US gov’t applications require a SHA-2 hash

SHA-3

Intent is for it NOT to derive (or be similar to) SHA-2
- So if the SHA-1 vulnerability exists in SHA-2, it thus will not affect SHA-3
NIST (National Institute for Standards and Technology) had an open solicitation / compettion for the algorithm
- The particular one selected was Keccak

Storing passwords

No (secure) system stores user passwords in plaintext
Instead it stores a hash of those passwords
- On login, it hashes your attempt, and then compares the hashes
- Thus, there could be multiple passwords that would log you in
This leads to vulnerabilities…

Dictionary attacks

To perform a dictionary attack:
- Take every hashed password for a given system
- Take every word in the English language, and hash it
- Find the intersection of those, and you have a bunch of passwords

Rainbow tables

A rainbow table is a pre-computed list of all hashed passwords
- Here is the one for ‘password’
They are searchable (by hash) via Google

Password Salting

To prevent dictionary attacks, and limit the usefulness of rainbow tables, passwords are salted
Each password is given a random number, or salt, which is added to the hash

Password Salting Example

Normally, ‘password’ has MD5 hash of 5f4dcc3b5aa765d61d8327deb882cf99
Adding a random salt: ‘password935723798539’ has MD5 hash of 80d2b285e1d5e9b3078383a2e96074bf
- With a reasonable size salt, rainbow tables and dictionary attacks are of less use due to the search space size

Applied Cryptography

Openssl to generate a RSA Key

$ openssl genpkey -algorithm RSA \
    -pkeyopt rsa_keygen_bits:2048 \
    -out key.pem
....+++++
....+++++
$

PEM key file format

$ cat key.pem
-----BEGIN PRIVATE KEY-----
MIIEvwIBADANBgkqhkiG9w0BAQEFAASCBKkwggSlAgEAAoIBAQDKmfQPMEZiho43
7rYfHB6bXDW1aQWrSJLlufEB23akwgyiHI85XcejJ10prWGU8aJA4VW8UJ1e6EZu
m0LFln1LCEZJX1Os/H9zR2OxV52Xd+/U5ooy+nxg9VfBwUOcEx6gmNfQu06zLDuf
cyKWXkF3DOE7rlPSq1xLk0GxYq+VvQEexMphMswdIiqcx4swdDWdA7x7z/nX6opx
TDp+tY3M/QIJVh6mn1MvIbhc+PDLQRvEi1ZhMiAgk69LkA32gxXFaSU+x5Cl44dH
69SJX3Z3xVhy/dpRpac9yEf/iVbSyV9z7as2qcD7PEfa3vIiQ+5o1O3O0jG40d8T
bxCsPe7TAgMBAAECggEBAJ3AVBWDfDp5FMGeYDZG+dn0aWlwddaRcrfnGS5eCLpu
0dFkNWzwhWKXYuXxt3p2zuR/z/cKOg7NAxJaWBpre/FxZvD4hbm6/S3wl0JduzpW
S+rU+ySIf1IrloIqDo+3H3DisaA4SCYguegEiRjWGVkuMS38Jg5yGTJLXapV8eu/
VGetSD7o6icG3QUs44NUOgoDPJeM41WpndgqPl558p6Y0wo48o08GBnQ7eAn+ERW
06JBeQ70/lrsj0RbkJdBqou17O2fpTJW0MM4fEWa9c8DCWmQIIS2R17sZNIT2/i1
9hnMWnvu5N+cIU53zefpskzmv6VdDLa0o1prqvvmlEECgYEA87t8HnvI1RzSvJUe
+/Knioe2PK9Ebd6HMJjNPhzuHOGjSDVbxMmBmDuxFgA7ia/PRGQLKUPcqlMBEJo+
C8t7gyAa5v8kJFvn8Y1+gdRkVqV/g7yV8Bes/0ZbDNzHra4vOVzkIO+gopy/9/Iz
CmSBP56p4/VUV5MC4l6OeTTHJPMCgYEA1Mx955btDWa8vqJJCsXcNp+Av1J9dI2e
T3Jx2/7ETNTCAD98r/2PryboHq1R20DqE/lTWE06gOphHl1OOyoR8YaV7zT0bzlP
4DoTvxamp7Xah8mgnnG0FjGSclKeMSeFsQAIfX+VJGqw+8UWTHgVsu+B8OQCHQ1n
wIZ3mp/WBqECgYAqhAHar20Q/74i90A4YtOm7pVzcH9XSwH6EC19MD64+wMojWY8
pYndrEvvsoqwMeLN40WvJQ9RBrmg08cO96fL78XBlbAQR5fmIvB2ZT47fxMHP9ZH
01lyDivDyp9qRIAoWXPR6vryYrV54t3UakPBfUPVZ+4WeKaAJk5kBjjW0QKBgQCb
19ctUD7zXZZFFpzfouAPsOidNVBjl4OlM29nakFg8z/Q5q3uRYiBAcFlFhGovPWx
Axuiw4xg9UWC81pjwf+6HpKXyPRqsFJrKJ1liLUsheYxI9zZrPPyfQN/bjokTYl/
g0K0hkc3kFtlR4V5I0jg7r7/KDzUAglF2jSlrQEVgQKBgQCVbKjqCbDzTIrct8jQ
xVrEpND1JcnyQoAdBIi8Lf8ffVpCxBhOBklJhhXqjaZ8iE7nS7xWfDOR2Jm0RUu0
3KpnWcKQz7MCGjkXVWrm412T1lrnp2UlD0MhqLps27NUJ6bybr200kwHxJcrZLb0
p4ZuGFwSn9QTFdGG3Y/OPRGWhg==
-----END PRIVATE KEY-----
$

OpenSSL to view a RSA Key

$ openssl rsa -in key.pem -text -noout
RSA Private-Key: (2048 bit, 2 primes)
modulus:
    00:ca:99:f4:0f:30:46:62:86:8e:37:ee:b6:1f:1c:
    1e:9b:5c:35:b5:69:05:ab:48:92:e5:b9:f1:01:db:
    76:a4:c2:0c:a2:1c:8f:39:5d:c7:a3:27:5d:29:ad:
    61:94:f1:a2:40:e1:55:bc:50:9d:5e:e8:46:6e:9b:
    42:c5:96:7d:4b:08:46:49:5f:53:ac:fc:7f:73:47:
    63:b1:57:9d:97:77:ef:d4:e6:8a:32:fa:7c:60:f5:
    57:c1:c1:43:9c:13:1e:a0:98:d7:d0:bb:4e:b3:2c:
    3b:9f:73:22:96:5e:41:77:0c:e1:3b:ae:53:d2:ab:
    5c:4b:93:41:b1:62:af:95:bd:01:1e:c4:ca:61:32:
    cc:1d:22:2a:9c:c7:8b:30:74:35:9d:03:bc:7b:cf:
    f9:d7:ea:8a:71:4c:3a:7e:b5:8d:cc:fd:02:09:56:
    1e:a6:9f:53:2f:21:b8:5c:f8:f0:cb:41:1b:c4:8b:
    56:61:32:20:20:93:af:4b:90:0d:f6:83:15:c5:69:
    25:3e:c7:90:a5:e3:87:47:eb:d4:89:5f:76:77:c5:
    58:72:fd:da:51:a5:a7:3d:c8:47:ff:89:56:d2:c9:
    5f:73:ed:ab:36:a9:c0:fb:3c:47:da:de:f2:22:43:
    ee:68:d4:ed:ce:d2:31:b8:d1:df:13:6f:10:ac:3d:
    ee:d3
publicExponent: 65537 (0x10001)
privateExponent:
    00:9d:c0:54:15:83:7c:3a:79:14:c1:9e:60:36:46:
    f9:d9:f4:69:69:70:75:d6:91:72:b7:e7:19:2e:5e:
    08:ba:6e:d1:d1:64:35:6c:f0:85:62:97:62:e5:f1:
    b7:7a:76:ce:e4:7f:cf:f7:0a:3a:0e:cd:03:12:5a:
    58:1a:6b:7b:f1:71:66:f0:f8:85:b9:ba:fd:2d:f0:
    97:42:5d:bb:3a:56:4b:ea:d4:fb:24:88:7f:52:2b:
    96:82:2a:0e:8f:b7:1f:70:e2:b1:a0:38:48:26:20:
    b9:e8:04:89:18:d6:19:59:2e:31:2d:fc:26:0e:72:
    19:32:4b:5d:aa:55:f1:eb:bf:54:67:ad:48:3e:e8:
    ea:27:06:dd:05:2c:e3:83:54:3a:0a:03:3c:97:8c:
    e3:55:a9:9d:d8:2a:3e:5e:79:f2:9e:98:d3:0a:38:
    f2:8d:3c:18:19:d0:ed:e0:27:f8:44:56:d3:a2:41:
    79:0e:f4:fe:5a:ec:8f:44:5b:90:97:41:aa:8b:b5:
    ec:ed:9f:a5:32:56:d0:c3:38:7c:45:9a:f5:cf:03:
    09:69:90:20:84:b6:47:5e:ec:64:d2:13:db:f8:b5:
    f6:19:cc:5a:7b:ee:e4:df:9c:21:4e:77:cd:e7:e9:
    b2:4c:e6:bf:a5:5d:0c:b6:b4:a3:5a:6b:aa:fb:e6:
    94:41
prime1:
    00:f3:bb:7c:1e:7b:c8:d5:1c:d2:bc:95:1e:fb:f2:
    a7:8a:87:b6:3c:af:44:6d:de:87:30:98:cd:3e:1c:
    ee:1c:e1:a3:48:35:5b:c4:c9:81:98:3b:b1:16:00:
    3b:89:af:cf:44:64:0b:29:43:dc:aa:53:01:10:9a:
    3e:0b:cb:7b:83:20:1a:e6:ff:24:24:5b:e7:f1:8d:
    7e:81:d4:64:56:a5:7f:83:bc:95:f0:17:ac:ff:46:
    5b:0c:dc:c7:ad:ae:2f:39:5c:e4:20:ef:a0:a2:9c:
    bf:f7:f2:33:0a:64:81:3f:9e:a9:e3:f5:54:57:93:
    02:e2:5e:8e:79:34:c7:24:f3
prime2:
    00:d4:cc:7d:e7:96:ed:0d:66:bc:be:a2:49:0a:c5:
    dc:36:9f:80:bf:52:7d:74:8d:9e:4f:72:71:db:fe:
    c4:4c:d4:c2:00:3f:7c:af:fd:8f:af:26:e8:1e:ad:
    51:db:40:ea:13:f9:53:58:4d:3a:80:ea:61:1e:5d:
    4e:3b:2a:11:f1:86:95:ef:34:f4:6f:39:4f:e0:3a:
    13:bf:16:a6:a7:b5:da:87:c9:a0:9e:71:b4:16:31:
    92:72:52:9e:31:27:85:b1:00:08:7d:7f:95:24:6a:
    b0:fb:c5:16:4c:78:15:b2:ef:81:f0:e4:02:1d:0d:
    67:c0:86:77:9a:9f:d6:06:a1
exponent1:
    2a:84:01:da:af:6d:10:ff:be:22:f7:40:38:62:d3:
    a6:ee:95:73:70:7f:57:4b:01:fa:10:2d:7d:30:3e:
    b8:fb:03:28:8d:66:3c:a5:89:dd:ac:4b:ef:b2:8a:
    b0:31:e2:cd:e3:45:af:25:0f:51:06:b9:a0:d3:c7:
    0e:f7:a7:cb:ef:c5:c1:95:b0:10:47:97:e6:22:f0:
    76:65:3e:3b:7f:13:07:3f:d6:47:d3:59:72:0e:2b:
    c3:ca:9f:6a:44:80:28:59:73:d1:ea:fa:f2:62:b5:
    79:e2:dd:d4:6a:43:c1:7d:43:d5:67:ee:16:78:a6:
    80:26:4e:64:06:38:d6:d1
exponent2:
    00:9b:d7:d7:2d:50:3e:f3:5d:96:45:16:9c:df:a2:
    e0:0f:b0:e8:9d:35:50:63:97:83:a5:33:6f:67:6a:
    41:60:f3:3f:d0:e6:ad:ee:45:88:81:01:c1:65:16:
    11:a8:bc:f5:b1:03:1b:a2:c3:8c:60:f5:45:82:f3:
    5a:63:c1:ff:ba:1e:92:97:c8:f4:6a:b0:52:6b:28:
    9d:65:88:b5:2c:85:e6:31:23:dc:d9:ac:f3:f2:7d:
    03:7f:6e:3a:24:4d:89:7f:83:42:b4:86:47:37:90:
    5b:65:47:85:79:23:48:e0:ee:be:ff:28:3c:d4:02:
    09:45:da:34:a5:ad:01:15:81
coefficient:
    00:95:6c:a8:ea:09:b0:f3:4c:8a:dc:b7:c8:d0:c5:
    5a:c4:a4:d0:f5:25:c9:f2:42:80:1d:04:88:bc:2d:
    ff:1f:7d:5a:42:c4:18:4e:06:49:49:86:15:ea:8d:
    a6:7c:88:4e:e7:4b:bc:56:7c:33:91:d8:99:b4:45:
    4b:b4:dc:aa:67:59:c2:90:cf:b3:02:1a:39:17:55:
    6a:e6:e3:5d:93:d6:5a:e7:a7:65:25:0f:43:21:a8:
    ba:6c:db:b3:54:27:a6:f2:6e:bd:b4:d2:4c:07:c4:
    97:2b:64:b6:f4:a7:86:6e:18:5c:12:9f:d4:13:15:
    d1:86:dd:8f:ce:3d:11:96:86
$

Openssl to generate and view an ECDSA Key

$ openssl ecparam -out ec_key.pem -name secp256k1 -genkey
$ cat ec_key.pem 
-----BEGIN EC PARAMETERS-----
BgUrgQQACg==
-----END EC PARAMETERS-----
-----BEGIN EC PRIVATE KEY-----
MHQCAQEEIGcgMEVvdpER8E/FsnK2CsUWJWy9X39WLHdDtvFHCx8zoAcGBSuBBAAK
oUQDQgAE3jzNUf91RHMzRiob3KZLZI3BFcxZMg7UeHrM6ifVAjTNcBi9iqwYlCy8
LYKcHMYYna0smEOaQL6o0oPDV2hh9w==
-----END EC PRIVATE KEY-----
$

Openssl to view an ECDSA key

$ cat ec_key.pem
read EC key
Private-Key: (256 bit)
priv:
    67:20:30:45:6f:76:91:11:f0:4f:c5:b2:72:b6:0a:
    c5:16:25:6c:bd:5f:7f:56:2c:77:43:b6:f1:47:0b:
    1f:33
pub:
    04:de:3c:cd:51:ff:75:44:73:33:46:2a:1b:dc:a6:
    4b:64:8d:c1:15:cc:59:32:0e:d4:78:7a:cc:ea:27:
    d5:02:34:cd:70:18:bd:8a:ac:18:94:2c:bc:2d:82:
    9c:1c:c6:18:9d:ad:2c:98:43:9a:40:be:a8:d2:83:
    c3:57:68:61:f7
ASN1 OID: secp256k1
$

Private key (scalar) $d \approx 4.66 \ast 10^{76}$
Public key (point) $Q \approx (1.01 \ast 10^{76}, 9.29 \ast 10^{76})$

Top 10 uncracked codes

10. D’agapeyeff Cipher

A “challenge cipher” at the end of a 1939 book on cryptography
The author forgot how he encrypted it (and what it meant)
Many think that he made a mistake during encryption, hence why it has not been solved

9. Kryptos

A monument in the CIA headquarters, erected in 1990
In 1999, the first person publically admitted to solving about 90% of it
The other 10% remains unsolved (even by gov’t cryptographers)

8. Shugborough Hall Inscription

Based (somewhat) on a painting, but with a few differences
Has the following inscription:
D O.U.O.S.V.A.V.V. M
Is involved in the Holy Grail legend

7. Chinese Gold Bar Cipher

Gold bars issued to a General Wang in 1933
It supposedly is a deposit greater than $300 billion
But the bank is unknown

6. Chaocipher

An ‘unbreakable’ cipher from 1918
The gov’t was rather uninterested in it

5. The Dorabella Cipher

A letter from Edward Elgar to Dora Penny in 1897 - she never figured it out, either
87 characters from 24 symbols
Analysis indicates a frequency that would be expected from a substitution cipher

4. Beale Ciphers

According to the story, a man in 1820 buried a load of treasure in VA
One of the ciphers has been decrypted, and it details the treasure itself
Perhaps the others lead to the treasure…

3. Linear A

A script used in ancient Crete
- This is from 1450 B.C.
It is somewhat similar to Linear B, and thus some info on this tablet is understood
But not all…

2. Voynich Manuscript

An entire book in a secret script that is at least 400 years old
- 272 pages, although about 30 are missing
Lists unidentified plants, as well as herbal recipies, astrological diagrams
Has an ‘alphabet’ of 20-30 glyphs
Written in a ‘confident’ style - perhaps a hoax
Nobody has deciphered a single word

1. The Phaistos Disk

Also from ancient Crete
- And found along with Linear A
An inscription of hieroglyphics
Theories: a religious hymn, a list of soldiers, or a document about the building of a palace

CS 3710

Introduction to Cybersecurity

Encryption

Introduction

Telnet and tcpdump

Codes versus Ciphers

Codes

Codes

Security through obscurity

Block-ciphers vs. stream ciphers

Cipher Taxonomy

Classical ciphers and rotor machines

Caesar Cipher

Caesar Cipher

Caesar Cipher analysis

Caesar Cipher analysis

Cracking a substitution cipher

Vigenere cipher

Vigenere cipher table

Vigenere cipher

Vigenere cipher

Vigenere cipher result

Vigenere cipher analysis

One-time pad (OTP)

One-time pad (OTP) analysis

One-time pad (OTP) analysis

Re-using a one-time pad

Route cipher

Rail fence cipher

WW2 Navajo Code Talkers

WW2 Navajo Code Talkers

Rotor machines

Rotor machines

Enigma machine

Enigma machine

Private key “symmetric” ciphers

Data Encryption Standard (DES)

Cracking Triple DES encryption

DES conspiracy theories

Advanced Encryption Standard (AES)

AES Overview

Key Round Schedule

AES: SubBytes step

AES: ShiftRows step

AES: MixColumns step

AES: AddRoundKey step

AES Overview

Number Theory

Is that number prime?

Is that number prime?

Is that number prime?

More on the Fermat primality test

More on the Fermat primality test

Google’s recruitment campaign

How to compute \(a^e\text{ mod }n\) ?

Compute \(a^{1652} \text{ mod } n\)

Compute \(a^{1652} \text{ mod } n\)

Running the Fermat primality test

Primarily test conclusions

Bit size

The prime number theorem

RSA

Private key cryptography

Public key cryptography

Public key cryptography goals

RSA

Key generation steps

Key generation, step 1

Key generation, step 1

Key generation, step 1

Key generation, step 1

Key generation, step 1

Key generation, step 1

Key generation, step 2

Key generation, step 2

Key generation, step 3

Key generation, step 3

Key generation, step 4

The keys

Encrypting messages