# Contents [Formal grammars](#/formal) [Regular expressions](#/re) [NFAs](#/nfas) [REs to NFAs](#/res2nfas) [NFAs to DFAs](#/nfas2dfas) [Lex](#/lex)
# Formal Grammars
## Language Specification - Definitions of a [formal grammar](http://en.wikipedia.org/wiki/Formal_grammar) - A grammar is a four-tuple $G = (N, \Sigma, P, S)$ where: - $N$ is a finite set of non-terminal symbols - Σ is a finite set of terminal symbols - $P$ is a set of transitions: a finite subset of $(N \cup \Sigma) ^\* N(N \cup \Sigma) ^\* \rightarrow (N \cup \Sigma )^\*$ - $S$ is a special symbol $(S \in N)$ called the start symbol - An element $(a, b)$ is generally written as $a \rightarrow b$ and is called a production ======================================== ## Language Specification - Chomsky Hierarchy: 4 types of grammars - Type 3: A grammar is said to be *regular* if each production in $P$ is of the form $A \rightarrow B$ or $A \rightarrow x$, where $A, B, \in N$ and $x \in \Sigma*$ - Single non-terminal on the left, and one terminal and one non-terminal on the right - Example: regular expressions - Can be recognized by a finite state automata ======================================== ## Language Specification - Chomsky Hierarchy: 4 types of grammars - Type 2: A grammar is said to be *context free* if each production in $P$ is of the form $A \rightarrow \alpha$ where $\alpha \in (N \cup \Sigma)*$ - Right side can be a set of terminals and non-terminals - The syntax for most programming languages - Can be recognized by a push-down automata ======================================== ## Language Specification - Chomsky Hierarchy: 4 types of grammars - Type 1: A grammar is said to be *context sensitive* if each production in $P$ is of the form $\alpha \rightarrow \beta$, where $|\alpha| \le |\beta|$, and $\alpha, \beta \in N(N \cup \Sigma)*$ - The left side has non-terminals, so it can only be used depending on the context - Can be recognized by a linear bounded automata ======================================== ## Language Specification - Chomsky Hierarchy: 4 types of grammars - Type 0: A grammar with no restrictions is called unrestricted - Can be recognized by a Turing machine ======================================== ## Context free vs Context sensitive - Consider the follow CSV file: ``` 01,jqd1a,"Doe,John" 02,mst3k,"Mystery Science Theater 3000" ``` - How many columns are in the first row? The second? - How should we interpret the comma in the name in the first row? - Because it's in double-quotes, it's intended to be a comma inside a field, rather than a field separator - In other words, the context of where it occurs (in quotes or not) will dictate how it is interpreted ======================================== ## Context free vs Context sensitive - Consider the follow CSV file: ``` 01,jqd1a,"Doe,John" 02,mst3k,"Mystery Science Theater 3000" ``` - A context-free language would interpret the first row to have four columns: ``` 01 asb2t "Doe John" ``` - Whereas a context-sensitive language would interpret the first row have three columns: ``` 01 jqd1a Doe,John ``` ======================================== ## Operations on Languages - Given two languages L and M - $L \cup M = \\{s | s \in L \text{ or } s \in M \\}$ - $LM = \\{st | s \in L \text{ and } t \in M \\}$ - Kleene Closure: $L* = \bigcup_{i=0}^nL^i$ - Positive Closure: $L+ = \bigcup_{i=1}^nL^i$ - Note the $i=1$ instead of $i=0$
# Regular Expressions
## Regular Expressions - $e$ is a regular expression denoting $\\{e\\}$, the language containing the empty string. ======================================== ## Regular Expressions - $R$ and $S$ are regular expressions denoting the languages $L\_R$ and $L\_S$ then - $(R) | (S)$ means $L_R \cup L_S$ - $(R) \cdot (S)$ means $L_R L_S$ - $(R)^\*$ means $L_R^\*$ - Notes - $^\*$ has the highest precedence and is left associative - $\cdot$ (concatenation) has the 2nd highest precedence and is left associative - $|$ has the lowest precedence and is left associative. ======================================== ## Regular Expressions: example - Let $\Sigma = \\{a, b\\}$ - $a | b \Rightarrow \\{ a, b \\}$ - $(a | b) (a | b) \Rightarrow \\{ aa, ab, ba, bb \\}$ - $a^\* \Rightarrow \\{e, a, aa, aaa, aaaa, \ldots\\}$ - $(a | b)^\* \Rightarrow $ all strings containing zero or more instances of a's and b's - $a | a^\*b \Rightarrow \\{ a, b, ab, aab, aaab, \ldots \\}$ ======================================== ## The previous example as a regex - While the two context-free slides properly describe context, it turns out that such a CSV file can actually be recognized by a regular expression: ``` (,("((\\")|([^"]))*")|[]|[^",]|([^"][^,"]*[^"]))* ```
# Non-deterministic Finite Automata
## Non-deterministic Finite State Automata - A non-deterministic finite automaton is a 5-tuple: $M = (Q, \Sigma, \delta, q_0, F)$ - where: - $Q$ is a finite set of states - $\Sigma$ is a finite set of permissible input symbols - $\delta$ is a mapping from $Q \times \Sigma \rightarrow P(Q)$ - $q_0 \in Q$ the initial state - $F \subseteq Q$ is the set of final states ======================================== ## Non-deterministic Finite State Automata - The automaton operates by making a sequence of moves - A move is determined by a current state and the symbol under the read head - A move is a change of state and moving the read head. ======================================== ## Representations of Automata Transition Diagram: 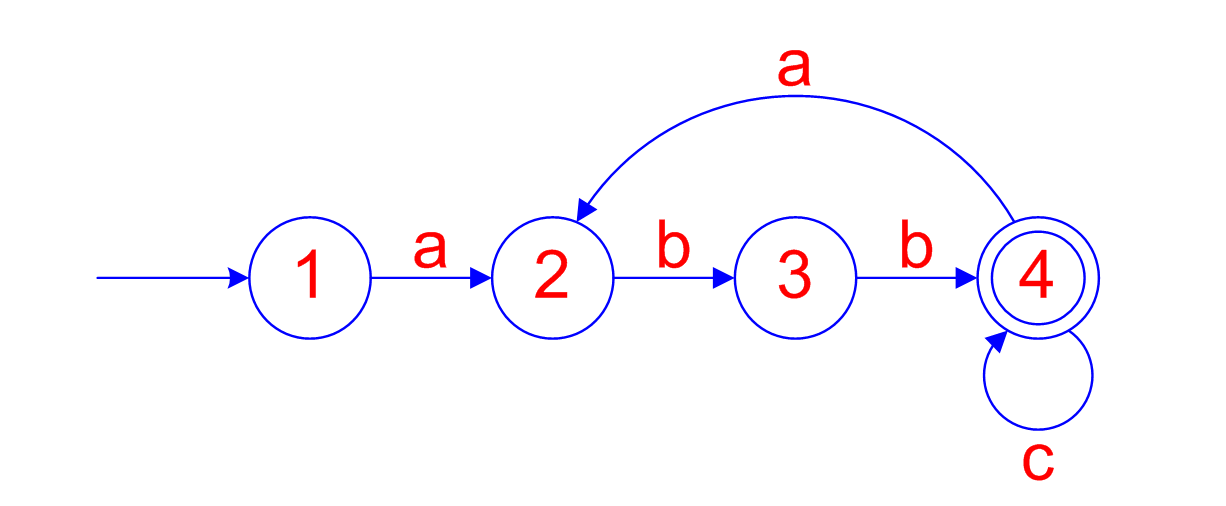 ======================================== ## Representations of Automata Transition Table: | State | | Input | | |-----|-----|-----|-----| | | a | b | c | | 1 | 2 | - | - | | 2 | - | 3 | - | | 3 | - | - | 4 | | 4 | 2 | - | 4 | ======================================== ## Non-determinism Transition Diagram: 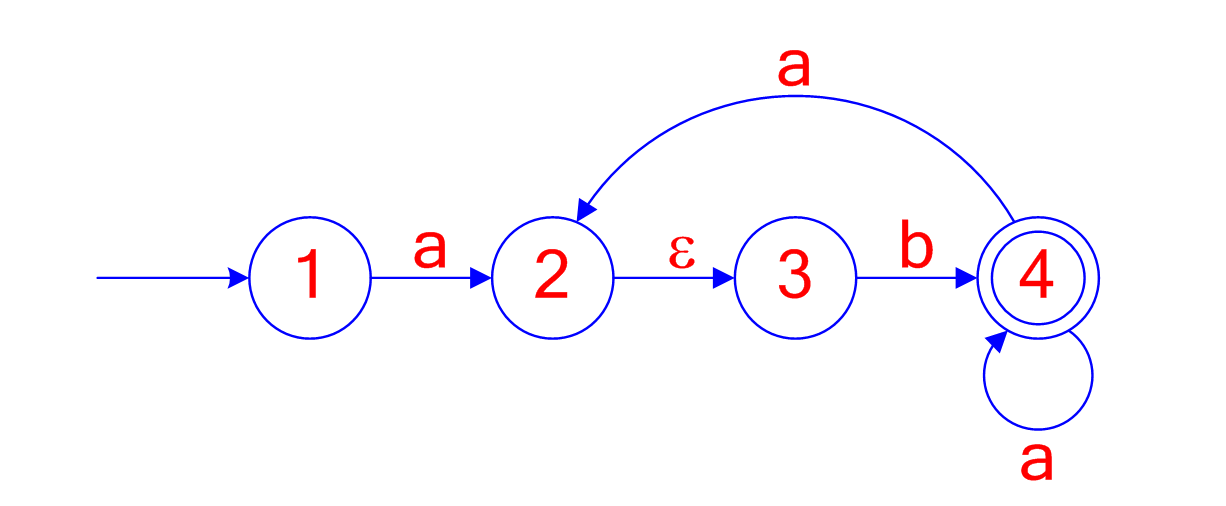 ======================================== ## What is an NFA? - A finite automata (FA) is a NFA (non-deterministic finite automata) if either: - There exists at least one empty transition $e$ - For any one state, there are multiple outgoing transitions for the same input symbol - If *neither* of these occur, then it's a DFA (deterministic finite automata)
# Converting REs to NFAs
## Converting a RE to a NFA - Each RE rule has a NFA equivalent - $e$ is  - $R_1|R_2$ is 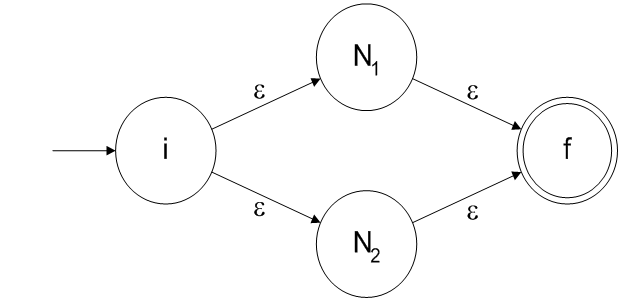 ======================================== ## Converting a RE to a NFA - $a$ is  - $R_1^\*$ is 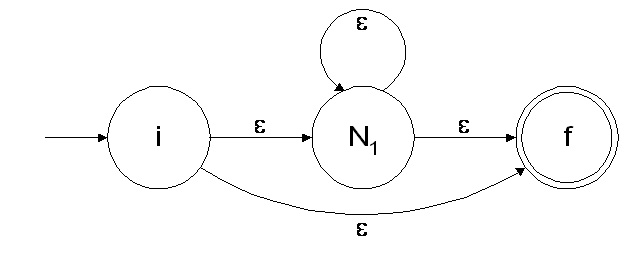 ======================================== ## Converting a RE to a NFA - $R_1R_2$ is 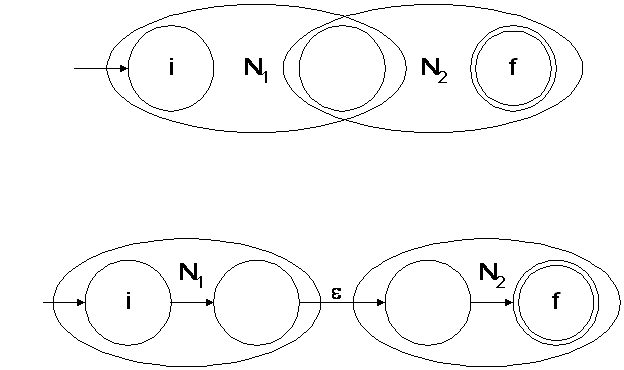 ======================================== ## Decomposition of (ab|ba)a* 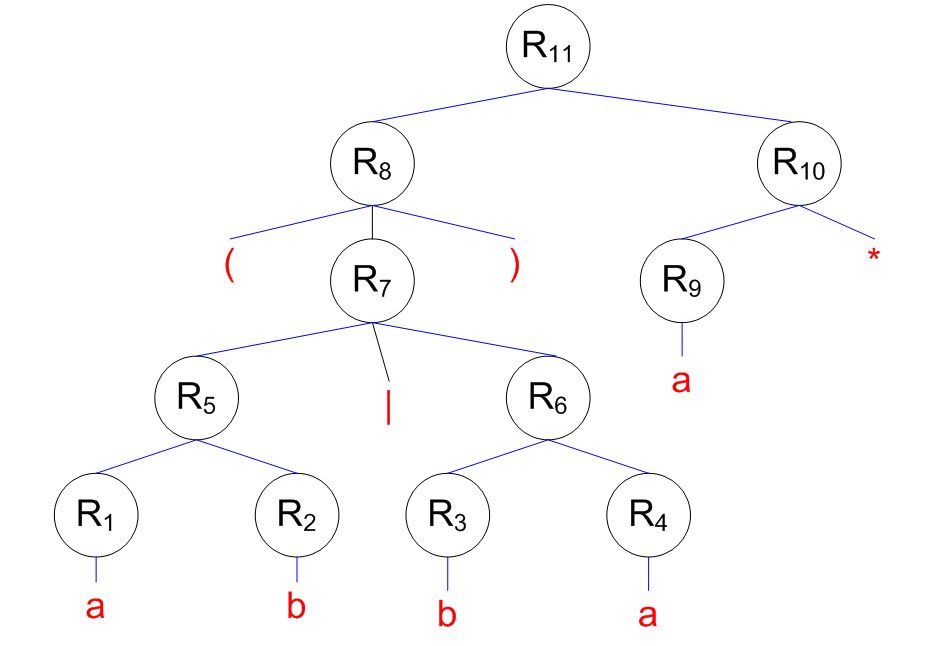 ======================================== ## Decomposition of (ab|ba)a* 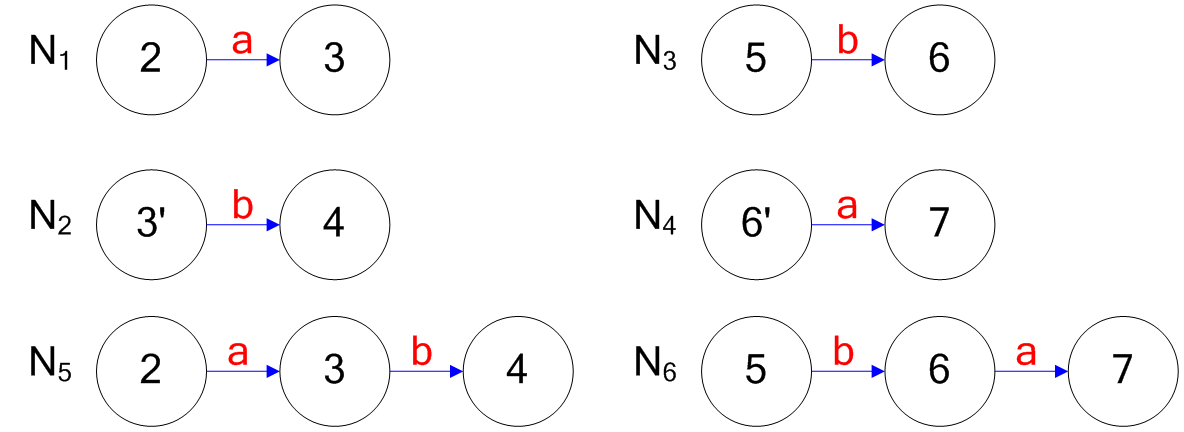 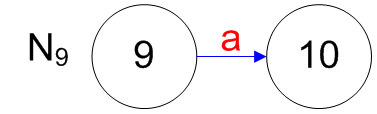 ======================================== ## Decomposition of (ab|ba)a* 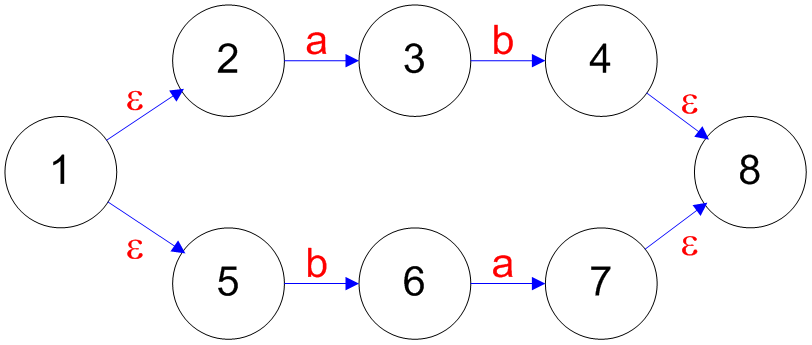 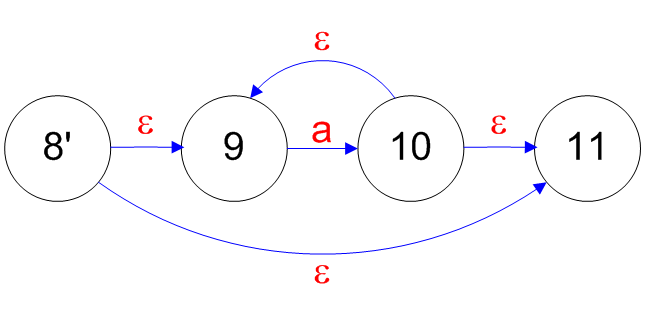 ======================================== ## Decomposition of (ab|ba)a* 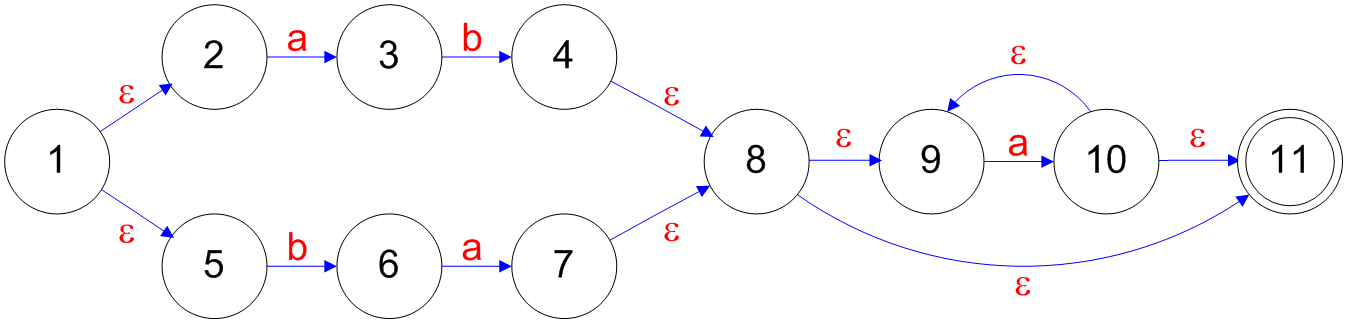
# Converting a NFA to a DFA
## Converting an NFA to a DFA - Each D-state is a set of N-states - Initial D-state = {$e$-closure(Initial(N-state))} - where: - $e$-closure(s) = $\\{ s \\} \cup \\{ t | s \rightarrow t$ on $e$-transition $\\}$ - Final D-states are those that hold final N-states. - Let D-states = {$e$-closure(Initial(N-state)}, unmarked ======================================== ## Converting an NFA to a DFA - While there is an unmarked D-state $X = \\{ s_1,\ldots,s_n \\}$ do - Mark $X$ - For each $a \in \Sigma$ do - Let $T$ = the states reached from some $s \in X$ by $a$ - Let $Y$ = $e$-closure($T$) - If $Y \notin$ D-states then - Add $Y$ to D-states, unmarked - Add a transition from $X$ to $Y$ labeled $a$ if one doesn't exist - Mark final states of D ======================================== ## Converting NFA to DFA - A = $e$-closure({1}) = {1, 2, 5} - B = $e$-closure({3}) = {3} - $a: \\{ 1, 2, 5 \\} \rightarrow \\{ 3 \\}$ - C = $e$-closure({6}) = {6} - $b: \\{ 1, 2, 5 \\} \rightarrow \\{ 6 \\}$ 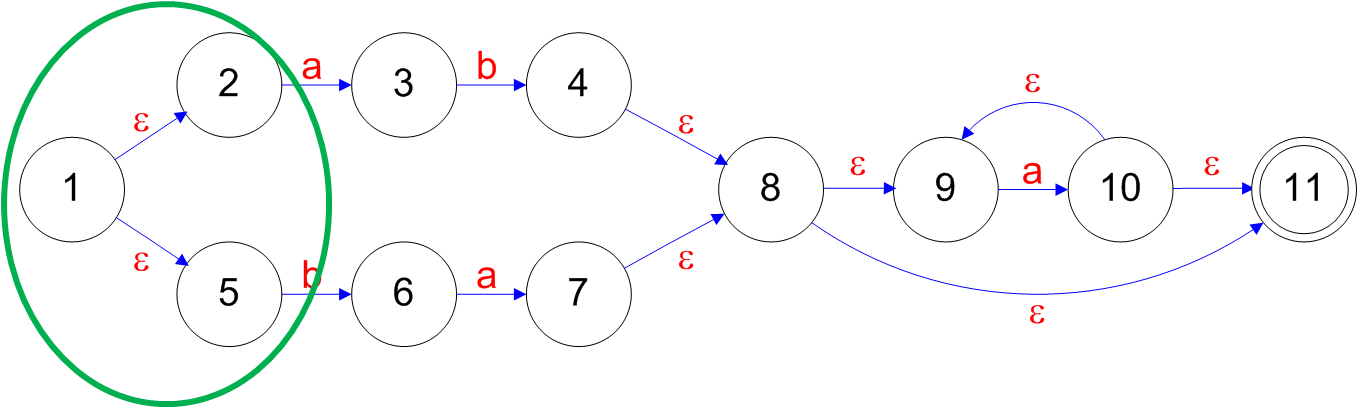 ======================================== ## Converting an NFA to a DFA - D = $e$-closure({4}) = {4, 8, 9, 11} - $b: \\{ 3 \\} \rightarrow \\{ 4, 8, 9, 11 \\}$ - E = $e$-closure({7}) = {7, 8, 9, 11} - $a: \\{ 6 \\} \rightarrow \\{ 7, 8, 9, 11 \\}$  ======================================== ## Converting an NFA to a DFA - F = $e$-closure({10}) = {9, 10, 11} - $a: \\{ 4, 8, 9, 11 \\} \rightarrow \\{ 9, 10, 11 \\}$ - $a: \\{ 7, 8, 9, 11 \\} \rightarrow \\{ 9, 10, 11 \\}$ - $a: \\{ 9, 10, 11 \\} \rightarrow \\{ 9, 10, 11 \\}$  ======================================== ## Converting an NFA to a DFA Yields the following automaton represented as a transition table: | | a | b | |--|--|--| |A|B|C| |B| |D| |C|E| | |D|F| | |E|F| | |F|F| | | ======================================== ## Converting an NFA to a DFA Yields the following deterministic automaton represented as an transition diagram: 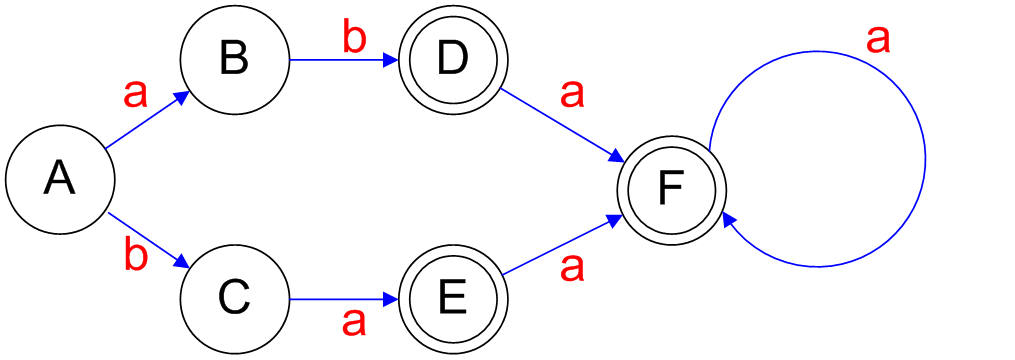
# Lex
## Lex - A Lexical Analyzer Generator - A way to specify regular expression rules for a grammar - C: http://www.lysator.liu.se/c/ANSI-C-grammar-l.html - Rules example: ``` /* regular expression */ /* action */ [ \t ]+$ ; ``` - This matches (and deletes) all blanks or tabs at the ends of lines (and then does nothing) ## Lex Lex source: ``` {definitions} %% {rules} %% {user subroutines} ``` Lex special characters: ``` " \ [ ] ^ - ? . * + | ( ) $ / { } % < > ``` ## Lex - Repeated expressions ``` a* a+ ``` - Character classes (matches any character in the range(s)): ``` [abc] [a-z] [a-zA-Z] [^abc] [^a-zA-Z] ``` - To include a - in a character class, it should be the first or last character in the class. ## Lex - Arbitrary character (but not newline): ``` . a.b ``` - Alternation: ``` ab|cd ``` - Context sensitivity: ``` ^ $ ab/cd ``` ## Lex ``` %{ /* * This sample demonstrates (very) simple * recognition: a verb/not a verb. */ %} %% [\t ]+ /* ignore whitespace */ is | am | are | were | was | be | being | been | do | does | did | will | would | should | can | could | has | have | had | go { printf("%s: is a verb\n", yytext); } [a-zA-Z]+ { printf("%s: is not a verb\n", yytext); } %% ``` ## Lex - Implementation Details - Construct NFA to recognize sum of Lex patterns. - Convert to DFA. - Minimize DFA, but separate distinct tokens in initial partition. - Simulate DFA to termination (i.e. no further transitions are possible). - Find last DFA state that holds an accepting NFS state. - This picks the longest match. - If no such DFA state exists, just output the character and go again. ## Disambiguating Rules - What happens if two rules match the same input? - Answer: Prefer the rule that appears first in the specification - Example: ``` foo { printf ("recognized 'bar'"); } [a-z]+ { printf ("recognized a word"); } ``` - If the input contained "foo", the output would be "bar" ## Disambiguating Rules - What happens if two rules could match different pieces of the input - Example: ``` is { printf ("recognized \"is\""); } island { printf ("recognized \"island\""); } ``` - Answer: Lex executes the action for the longest possible match for the current input. ## UVa userids - There are a few forms: - The original form: two or three letters ('ab', 'abc') - Two initials, a digit, and then one or two letters ('ab1c', 'ab1cd') - Three initials, a digit, and then one or two letters ('abc1d', 'abc1de') - A regex: ``` [a-z][a-z][a-z]?([0-9][a-z][a-z]?)? ``` ## Lex code - Source code: [uva-userid.l](code/05-re-and-lex/uva-userid.l) ``` USERID ^[a-z][a-z][a-z]?([0-9][a-z][a-z]?)?$ %% {USERID} { printf("Found a UVa userid: %s\n",yytext); } .|\n { /* ignore other input */ } %% ``` - In the regex, the `^` means the start of the line - And `$` means the end of the line - This prevents it from finding a userid in the string `abcdefg` ## Compiling and running - One can either use lex or flex (the "fast" version of lex) ``` flex uva-userid.l gcc lex.yy.c -lfl ``` - Since a `main()` wasn't included, lex puts one in for you - As you type input, it prints out either "found a uva userid" or nothing - The `fl` library (linked via `-lfl`) provides necessary functionality for this program to work ## What lex does - When you run `flex uva-userid.l`, it creates a 1,776 line file that will read in tokens - Result: [lex.yy.c](code/05-re-and-lex/lex.yy.c.html) ([source](code/05-re-and-lex/lex.yy.c)) - The `yy_accept` array is the state change table (there are others as well in the file): ``` static yyconst flex_int16_t yy_accept[13] = { 0, 0, 0, 4, 2, 2, 0, 1, 0, 0, 0, 0, 0 } ; ``` - The [C grammar](http://www.lysator.liu.se/c/ANSI-C-grammar-l.html), for comparison, generates a 2,448 line lex.yy.c