## Transaction Tracing
- Transactions on networks such as Ethereum and Bitcoin can be traced
    - All you need to trace a transaction is to track coins through (what may be multiple) wallets to determine where the coins originated
    - If the coins were purchased through an exchange, that exchange will have the personal information of the wallet that exchanged/purchased the coins
- Scammers or hackers will bounce the funds through many wallets so that it is harder to trace funds, but it is not impossible

## 2020 Twitter Hack
<img src='images/zksnarks/bill_gates_hacked.webp' class='stretch'>

## 2020 Twitter Hack
- In 2020, a scammer used a phishing attack to access 130 famous Twitter accounts and asked for Bitcoin donations with the promise of doubling any money sent ([ref](https://www.wired.com/story/how-alleged-twitter-hackers-got-caught-bitcoin/))
- They were able to get about `$`180,000 worth of Bitcoin
- Investigators were able to find the perpetrators by tracing the Bitcoin transactions back to Coinbase accounts

## Solutions
- In traditional financial systems, payment privacy is enforced by trusted third parties such as banks
  - However, this system is still vulnerable to [data breaches](https://www.upguard.com/blog/biggest-data-breaches-financial-services)
- If a company is paying its employees with cryptocurrencies, they want employee information, payment amounts, and company information to be private
- For a cryptocurrency to be completely private and encrypted, transactions must be fully verifiable with zero knowledge of what the transaction actually holds

## Example: The Ali Baba cave
![](images/zksnarks/Zkip_alibaba1.webp)
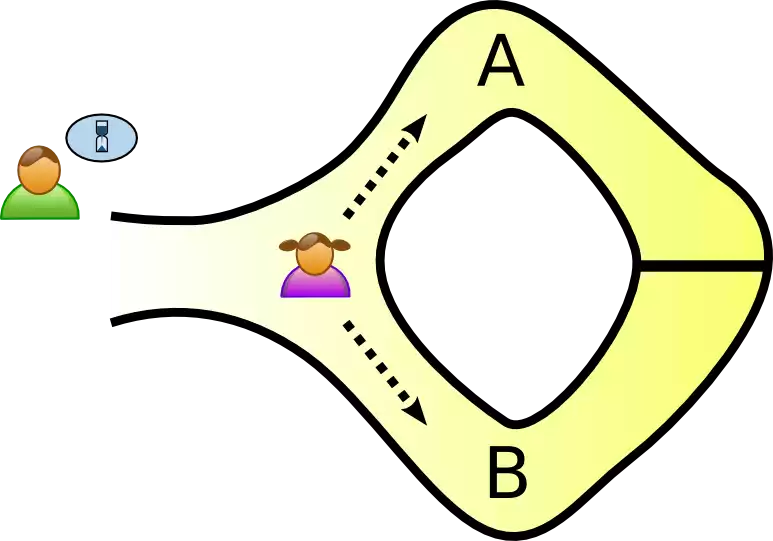- A circular cave has a locked door
- Peggy (the "prover") knows how to open it, and wants to prove it to Victor (the "verifier")
  - But she doesn't want Victor to see how to open it
- How can she prove this to him?
  - And not show it to the rest of the world?
- (Images from [Wikipedia](https://en.wikipedia.org/wiki/Zero-knowledge_proof))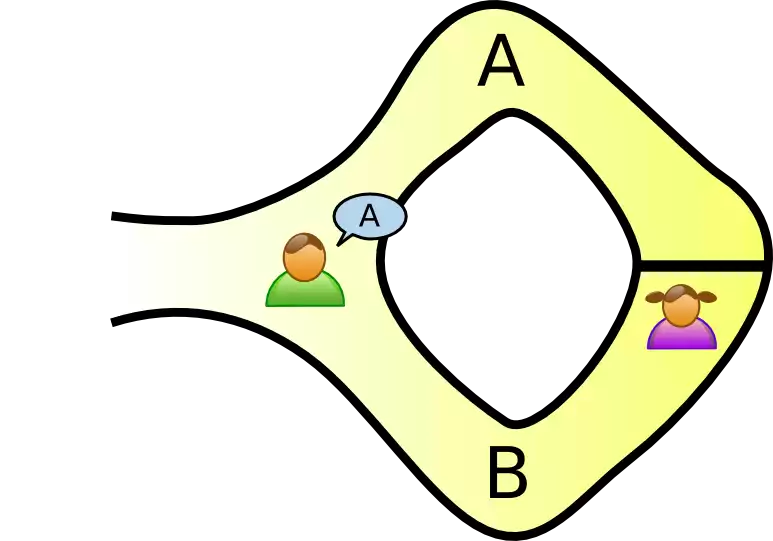

## Example: The Ali Baba cave
![](images/zksnarks/Zkip_alibaba1.webp)
- Victor waits outside, and Peggy randomly chooses path A or B

## Example: The Ali Baba cave
![](images/zksnarks/Zkip_alibaba2.webp)
- Victor waits outside, and Peggy randomly chooses path A or B
- Victor enters the cave, and states which path he wants Peggy to exit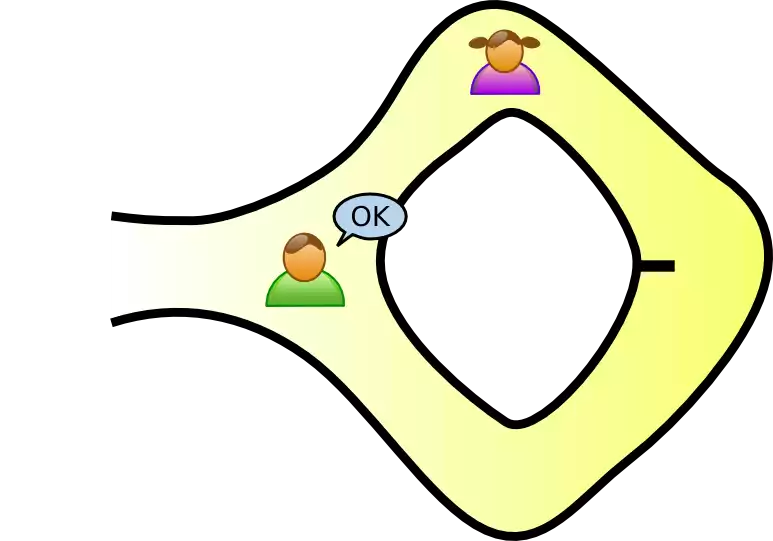

## Example: The Ali Baba cave
![](images/zksnarks/Zkip_alibaba3.webp)
- Victor waits outside, and Peggy randomly chooses path A or B
- Victor enters the cave, and states which path he wants Peggy to exit
- Peggy either:
  - Went down that path, and doesn't have to open the door
  - Went down the other path, and does have to open the door
- Each with 50% probability

## Results
- This shows, with 50% probability, that Alice knows a "key"
  - If run twice, then it shows with 75% probability
- To get a higher confidence level, run it many times
  - 10?  100? 1000?
- But this is not a proof!
  - Since there is a $\frac{1}{2^n}$ chance that Peggy was just really lucky
- We'll call it a *verification*
- Note that this is an *interactive* verification

## But wait...
- Why doesn't Victor check that the door is locked, and then have Peggy do a loop?
- Recall that Peggy wants to prove to Victor that she knows the key
  - But not show it to the rest of the world
- The current experiment:
  - Does convince Victor (with probability $1/2^n$ for $n$ tries)
  - Will look staged to the rest of the world
- Peggy doing a loop:
  - Will still convince Victor
  - Will reveal that Peggy knows the key to the rest of the world

## Where's Waldo
![](images/zksnarks/MartinHandfordWallyandFriends.webp)
- A series of illustrations in books by Martin Handford
- Each image is very busy, and one has to find Waldo
- If I know where Waldo is, I can prove it by showing you
- But how do I prove it without showing you his position?
- (Image from [Wikipedia](https://en.wikipedia.org/wiki/Where%27s_Wally%3F))

## Where's Waldo
- Let's do an example!
- This *is* a proof, since I can definitively show where Waldo is
  - There could be *multiple* Waldos, but I have still showed where one is
- This is still an *interactive* proof
  - Although I could leave it lying around, and it would be (mostly) non-interactive
- Note who I verified it to, though...

## Qualities of a Zero-Knowledge Proof
- *Completeness:* the verifier can be (almost) certain that the prover "knows" the information
  - After $n=100$ iterations, Peggy knows how to work the lock
  - I definitively know where Waldo is
- *Soundness:* the prover cannot "prove" false information to the verifier
  - After $n=100$, Peggy cannot (realistically) have faked it
  - I cannot have shared a false location of Waldo
- *Zero-Knowledge:* The information being proven by the prover is never shared to the verifier
  - Victor does not know how to work the lock
  - You do not find out where Waldo is

## Interactive ZK proofs
- The prover and verifier must interact for the verifier to be certain that the prover knows the secret
  - In the cave example, it required many iterations to verify
  - In the Where's Waldo example, the prover must show the verifier the hole cut out around Waldo to prove their knowledge

## Non-Interactive ZK proofs
- The prover can provide a verified account of their proof without having to interact with a verifier
    - The verifier in this case can be a random oracle which generate values to test the proof
    - This requires some form of a trusted random generation algorithm, often implemented by a cryptocurrency organization
- This means the majority of the work must be implemented by the prover and the verification step is easy for other nodes on the network

## zk-SNARKs
- zk-SNARK = **Z**ero **K**nowledge **S**uccinct **N**on-Interactive **AR**gument of **K**nowledge
- **Zero knowledge** so that transaction information is hidden from other nodes and tracing is thus not possible
- **Succinct** so that verifying transactions using this method does not take (substantially) longer than other blockchains
  - And the data transmitted is small
- **Non-Interactive** so that other nodes do not need to be active while proof is being generated
  - Also limits computation power/time for other nodes

## Goals
- Alice needs to *show* to Bob that she knows some secret piece of information
- Beyond the qualities of completeness, soundness, and zero-knowledge...
- We have two goals:
  - Blindness: Alice and Bob will not learn any information from each other
  - Verifiability: Alice is properly showing this, and not returning fake values, is essentially zero
- The combination of these two implies that Alice has to select her information ahead of time without knowing Bob's information
- We will refine these shortly...

## Overview
- We want to show that we can evaluate polynomials in a zero-knowledge way
  - If Alice has a polynomial $P$ and Bob has a value $x$, then Bob can receive $P(x)$ without Alice knowing $x$ and without Bob knowing $P$
- Given that, we take some arbitrary computation and encode it as a polynomial
  - Through something called an *arithmetic circuit*
  - This computation could be something that the only (known) solution is a private key
- Then we define the protocol for this type of proof

## Sources
- The explanation in this slide set follows that of [Zcash](https://z.cash/)
  - Specifically their [How It Works](https://z.cash/technology/) page
  - And also their "Explaining SNARKs" (parts [1](https://electriccoin.co/blog/snark-explain1/) through [7](https://electriccoin.co/blog/snark-explain7/))
- [![zec logo](../slides/images/logos/zec-coin-symbol.svg)](https://coinmarketcap.com/currencies/zcash/) ZCash (ZEC)
- Another coin that uses zkSNARKs is [![firo logo](../slides/images/logos/firo-coin-symbol.svg)](https://coinmarketcap.com/currencies/firo/) Firo (FIRO), aka Zcoin

## Homomorphic Hidings
- A *homomorphic* operation $T$ transforms set A into set B while preserving (some) operations on the elements of the set
  - If $a_1,a_2 \in A$ and $T(a_1),T(a_2) \in B$, and if $a_1 \oplus a_2 = x$, then $T(a_1) \oplus T(a_2) = T(x)$
- A *Homomorphic Hiding* is an encryption scheme $E(x)$ that has the following properties:
    - Given $E(x)$, it is hard to find $x$
    - $E(x) \ne E(y)$ if $x \ne y$
    - Given $E(x)$ and $E(y)$, is it possible to compute $E(x+y)$ and other linear combinations without knowing $x$ and $y$

## Homomorphic Hidings
- Alice knows $x$ and $y$, and wants to prove to Bob that $x+y=z$
- Consider the finite group $Z_p$ for some prime $p$
- We define $E(x)=g^x$ for a known $g$
  - This is easy to compute
  - But it is hard to determine $x$ from $g^x$ because discrete logs are hard
  - $g$ is the *generator* for $Z_p$
    - A *generator* is a number such that every number in $Z_p$ can be generated by raising $g$ to some power
- We now compute $E(x+y) = g^{x+y} \mod p $ $= g^x \ast g^y \mod p = E(x) \ast E(y)$

## Homomorphic Hidings
- $E(x+y) = g^x \ast g^y \mod p = E(x) \ast E(y)$
- Does it fulfill the homomorphic hiding properties?
    - Given $E(x)$, it is hard to find $x$
        - Yes, due to the hardness of discrete logs
    - $E(x) \ne E(y)$ if $x \ne y$
        - Yes, this will hold since, for $Z_p$, $p$ is a prime
    - Given $E(x)$ and $E(y)$, is it possible to compute $E(x+y)$ and other linear combinations without knowing $x$ and $y$
        - Yes, we saw how to do this

## Very Simple HH Example
- Alice wants to prove to Bob that she knows numbers $x$ and $y$ such that $x+y=9$
  - We'll say she knows $x=4$ and $y=5$
- We define $E(x)$ as $E(x) = 7^x$ in $Z_{11}$
  - 7 is a generator for $Z_{11}$
- Alice computes $E(4)=7^4 \mod 11 = 3$ and $E(5)=7^5 \mod 11 = 10$
  - She then sends 3 and 10 to Bob
- Bob computes $E(9) = 7^9 \mod 11 = 8$
- Bob verifies that $3 \ast 10 \mod 11 = 8$
- Thus, Bob knows that Alice knows two numbers that add to 9

## Not zero-knowledge!
- Given $E(x)$, Bob can choose random $x'$ and see if $E(x)=E(x')$
  - Using brute force, Bob can figure out $x$ from $E(x)$
  - Although that is computationally impractical in practice
- This would have been easy with our example on the previous slide due to the fact that it was a simple example
- Also, zkSNARKs are used to conceal verifier challenges rather than prover secrets

## Supported operations
- Our homomorphic hiding operation $E(x)=g^x$ supports addition
  - Meaning we can compute $E(x+y)$ from $E(x)$ and $E(y)$
  - Specifically because $E(x+y)=E(x) \ast E(y)$
  - Derivation: $E(x+y)=g^{x+y}=g^x \ast g^y = E(x) \ast E(y)$

## Supported operations
- It also supports *linear combinations*
  - Meaning we can compute $E(ax+by)$ from $E(x)$ and $E(y)$
  - Derivation:
    - $E(ax+by)=g^{ax+by}=g^{ax} \ast g^{by}=(g^x)^a \ast (g^y)^b$ $=E(x)^a \ast E(y)^b$
  - Note that this is not *polynomial* combinations
- It does *not* support general multiplication
  - We'll come back to that later

## Identities
- We note from these derivations the following identities:
  - $E(x+y)=E(x) \ast E(y)$
  - $E(ax)=E(x)^a$
- Specifically:
  - We can perform addition and scalar multiplication with our homomorphic hidings
  - But not general multiplication, such as of a polynomial by another polynomial

## Polynomial Encoding
- To create a zero-knowledge proof, we want to encode our information in polynomials
  - As verifiers will be able to prove that a polynomial is correct using homomorphic hidings.
- This is done by evaluating polynomials at certain values and checking if the output is equal to the correct solution
- A polynomial or degree $d$ is defined here as:

$$ P(x)=a_0+a_1 \ast x^1 + a2 \ast x^2 + \ldots a_d \ast x^d $$

For some $a_0, \ldots, a_d \in Z_p$

## Blind Polynomial Evaluation
- Alice knows a polynomial $P$ of degree $d$
- Bob randomly chose a value $x \in Z_p$, and wants to learn $E(P(x))$
- Two choices:
  - Alice sends $P$ to Bob, and he computes $E(P(x))$
    - This is not blind evaluation!
  - Bob sends $x$ to Alice, she computes $E(P(x))$ and sends it back to Bob
    - He does this by sending the hidings $E(1), E(x), \ldots, E(x^d)$ to Alice
    - She uses linear combinations of these to compute $E(P(x))$

## Blind Polynomial Evaluation
- Alice knows $P=x^2+3x+4$
- We'll keep using $E(x) = 7^x$ in $Z_{11}$
- Bob chose value $x=4$
  - Result: $4^2+3 \ast 4 + 4 = 32$ and $E(32)=5$
- Bob sends values $E(1)=7, E(4)=3, E(4^2)=4$
- Alice wants to compute $E(P(x))=E(x^2+3x+4)$
  - $= E(x^2) \ast E(3x) \ast E(4 \ast 1)$ 
    - as $E(x+y)=E(x) \ast E(y)$
  - $= E(x^2) \ast E(x)^3 \ast E(1)^4$ 
    - as $E(ax)=E(x)^a$
  - $= 4 \ast 3^3 \ast 7^4 \mod 11 = 5$
- Alice then sends 5 to Bob; and, indeed, $E(32)=5$

## Wait, what happened?
- Bob chose a random value $x=4$, and sent homomorphic hidings $E(x^n)$ to Alice (for $n=1 \ldots d$)
  - Bob did not reveal that $x$ equals 4 to Alice
- Alice knew a polynomial $P(x)$, and computed the value $E(P(x))$ for $x=4$, and sent the result back to Bob
  - Alice did not reveal the polynomial to Bob
- What is still left to explain:
  - How can Bob verify this?
  - Could Alice be faking this and just returning an arbitrary number?
  - Why is this useful?
- Rest, Neo.  The answers are coming.

## Goals, take 2
- Alice needs to *show* to Bob that she knows $P(x)$
- We have two goals with updated phrasing:
  - Blindness: Alice will not learn the $x$ that Bob submits, and Bob will not learn the $P(x)$ that Alice knows
    - This has been achieved
  - Verifiability: The chance that Alice is not properly returning $E(P(x))$ is essentially zero
    - We are not there yet...
- The combination of these two implies that Alice has to select $P$ before learning Bob's $E(x)$

## Forcing Alice to behave
- Bob needs to force Alice to not make up the results
- This is done via the Knowledge of Coefficient (KC) Test
- Overview:
  - Bob chooses two numbers $(a,b)$ that have a *linear* relationship, such as $b=\alpha \cdot a$
  - Alice cannot figure out the relationship because doing so is *hard* (read: computational infeasible)
  - Alice can, however, figure out $E(P(a))$ and $E(P(b))$
    - If Alice computes these faithfully, the relationship will be preserved
  - Bob, once receiving $(a',b')=(E(P(a)),E(P(b)))$ can verify that the linear relationship still exists

## The Knowledge of Coefficient (KC) Test
1. Bob chooses a random $\alpha \in Z_p$ and $a \in Z_p$
   - He computes $b=\alpha \cdot a$
2. Bob sends Alice the pair $(a,b)$
   - This is called an $\alpha$-pair since $b=\alpha \cdot a$
3. Alice computes $(a',b')$ where $a'=E(P(a))$ and $b'=E(P(b))$, and sends that to Bob
   - This is still an $\alpha$-pair if it was computed correctly
4. Bob verifies that $(a',b')$ is an $\alpha$-pair
   - He knows $\alpha$, so that's easy to do

## Computing alpha-pairs
- The operation to compute $\alpha$-pairs must not be reversible
  - Or not reversible *feasibly*
- So multiplication is out
  - As one can reverse it by doing division in a field
- But exponentiation is valid
  - As discrete logs are *hard*
- For simplicity in notation, we will use the center-dot notation: $\cdot$
- Formally, $x \cdot y \equiv y^x$ (mod $p$)
- For some of the explanations that follow, we'll use multiplication

## KC Test Example
- We still define $E(x)$ as $E(x) = 7^x$ in $Z_{11}$
- Bob chooses $a=4$ and $\alpha = 10$, so $b=\alpha \ast a = 10 \ast 4 = 7$ in $Z_{11}$
- Bob sends the HHs for pair $(4,7)$ to Alice:
  - For $a=4$: $E(1)=7, E(4)=3,E(4^2)=4$
  - For $b=7$: $E(1\cdot\alpha \text{ \% } 11)=1$, $E(7\cdot\alpha \text{ \% } 11)=6$, and $E(7^2\cdot\alpha \text{ \% } 11)=4$

## KC Test Example
- Alice doesn't know $(a,b)$, but computes & sends back:
  - $a'=E(P(a))=E(P(4))=5$
  - $b'=E(P(b))=E(P(7))=6$
  - Recall: $E(P(x))= E(x^2) \ast E(x^1)^3 \ast E(x^0)^4$ 
- Bob verifies that $(5,6)$ is an $\alpha$-pair

## Can Alice fake the KC Test?
- If Alice somehow knew $\alpha$, she could return $(a',b')=(a',\alpha \cdot a')$ for some $a' \in Z_p$
  - But she likely doesn't know $\alpha$, since it's random and Bob kept it secret
- Given $\alpha$-pair $(a,b)$, she can return $(a',b')=(\gamma \cdot a, \gamma \cdot b)$ for some $\gamma \in Z_p$
  - This $(a',b')$ is an $\alpha$-pair
- Thus, Alice will know $\gamma$ such that $a'=\gamma \cdot a$
  - Either because she made up a $\gamma$ it or because she divided $a'$ by $a$
  - More on this shortly

## Where we are
- Bob sends an $\alpha$-pair $(a,b=\alpha \cdot a)$ to Alice
  - Formally he sends the HHs for $(E(a),E(b))$
  - Alice does not know $\alpha$
- Alice responds with $(a',b')$, which also is an $\alpha$-pair
  - Maybe she evaluated her polynomial $P$ by returning $(a',b')=(E(P(a)),E(P(b))$
  - Or maybe she picked some $\gamma \in Z_p$ and returned $(a',b')=(\gamma \cdot a, \gamma \cdot b)$
- Either way, what she returns is indeed an $\alpha$-pair, which Bob verifies
- But Bob has to *also* ensure that Alice returned $(E(P(a)),E(P(b))$, not $(\gamma \cdot a, \gamma \cdot b)$ for some $\gamma \in Z_p$

## d-KCA
- Now let's imagine that Bob sends *two* $\alpha$-pairs: $(a_1,b_1)$ and $(a_2,b_2)$
- Alice could construct her return $(a',b')$ $\alpha$-pair by picking *two* different values, $\gamma_1$ and $\gamma_2$, to construct a return $\alpha$-pair:
  - $(a',b')=(\gamma_1 a_1+\gamma_2 a_2,\gamma_1 b_1 + \gamma_2 b_2)$

## d-KCA
- If Bob sent $d$ $\alpha$-pairs, then Alice could construct an $(a',b')$ $\alpha$-pair via linear combinations
- Bob chooses a random $\alpha \in Z_p$ and a random $x \in Z_p$
- Bob sends a series of $d$ $\alpha$-pairs:

$$(g,\alpha \cdot g),(x \cdot g,\alpha x \cdot g), \ldots ,(x^d \cdot g,\alpha x^d \cdot g)$$

- Specifically, these are the homomorphic hidings of $x^n$ for $0 \le n \le d$

## d-KCA
- Bob sends the homomorphic hidings for $x^n$
- Alice knows $P(x)$, but chooses not to use it
- Instead, Alice chooses some $\gamma_1,\ldots,\gamma_d \in Z_p$, and computes the following $\alpha$-pair:

$$(a',b') = ( \sum_{i=1}^d \gamma_i \cdot a_i, \sum_{i=1}^d \gamma_i \cdot b_i )$$

- Recall that $a_i$ (and, separately, $b_i$) are the homomorphic hidings for $x^n$ (and $(\alpha x)^n$)

## d-KCA
- Alice computes, for the homomorphic hidings of $a_i=E(x^i)$ and $b_i=E((\alpha x)^n)$:

$$(a',b') = ( \sum_{i=1}^d \gamma_i \cdot a_i, \sum_{i=1}^d \gamma_i \cdot b_i )$$

- She is computing a polynomial!
  - But not necessarily the *right* polynomial
  - Meaning not necessarily the $P$ that we are trying to verify

## Where we are
- By passing in the HHs for $x^n$ and $(\alpha x)^n$, Bob can force Alice to compute *a* polynomial
  - But not necessarily the $P(x)$ one that we want her to compute
- Next we have to ensure that she computes the *correct* one
  - Meaning the one showing that she controls her private key

## Protocol formalization
- The Verifiable Blind Evaluation Protocol:
  1. Given an agreed-upon $E(x)$, such as $E(x)=g^x$, Bob chooses a random $\alpha,x \in Z_p$, and sends the hidings of $g,x \cdot g,\ldots,x^d \cdot g$ and also $\alpha \cdot g,\alpha x \cdot g,\ldots,\alpha x^d \cdot g$
  2. Alice computes $a=E(P(x))$ and $b=E(\alpha P(x))$ using those values, and sends that to Bob
  3. Bob checks that $b = \alpha \cdot a$, and accepts only if true
- We still have a few issues to fix
  - Such as how to force Alice to compute the right polynomial

## Arithmetic circuits
- So far, we can evaluate polynomials with zero knowledge revealed
  - Although we have not yet seen how to force evaluation of the *correct* polynomial 
- We need to be able to convert a *computation* into a polynomial
  - Which we can then verify and compute with zero knowledge
- That computation might be the signing of a message of a hash with a private key
- We'll use: $(c_1 \cdot c_2) \cdot (c_1 + c_3)=7$

## Arithmetic Circuits
![](images/zksnarks/graphs/zksnarks.dot.1.svg)
- Suppose Alice wants to prove to Bob that she knows $c_1,c_2,c_3 \in Z_p$ such that $(c_1 \cdot c_2) \cdot (c_1 + c_3)=7$
  - If $\cdot$ is multiplication, then $(c_1,c_2,c_3)=(4,2,1)$ works
    - As does $(1,3,5)$, $(3,1,3)$, etc.
  - If $\cdot$ is exponentiation, then $(c_1,c_2,c_3)=(1,3,5)$ works
- We construct an *arithmetic circuit* as shown

## Arithmetic Circuits
![](images/zksnarks/graphs/zksnarks.dot.4.svg)
- Our updated graph 
  - Multiplication is a node, addition is "joining" of two inputs
  - Assume $c_1,\ldots,c_n$ flow left-to-right along the bottom
- We are going to model its *shape* using polynomials
- Given that:
  - The inputs $c_1,\ldots,c_n$ flow left-to-right along the bottom
  - The circular nodes are multiplication
  - The combining of edges is addition
- Then the resultant operation $(c_1 \cdot c_2) \cdot (c_1 + c_3)$ derives from this graph

## Arithmetic Circuits
![](images/zksnarks/graphs/zksnarks.dot.4.svg)
- We want to represent the *shape* of this graph with a polynomial
- The details are being skipped here
  - You can see them [later on]()
- So, POOF!  Some magic happens, and...
- The result is:
  - $P = (4x) \cdot (3x-1) - (-x+9) $ $= 12x^2-3x-9$
  - Somehow, $P$ represents the shape of this circuit
  - Although we won't see it here, $P$ is a sum of smaller polynomials $L$, $R$, and $O$
  - Specifically, $P=L(x) \cdot R(x)−O(x)$

## Where we are
- We have an equation $y=(c_1 \cdot c_2) \cdot (c_1 + c_3)$
- Alice wants to show that she knows $(c_1,c_2,c_3)$ such that $y=7$
- We converted the equation to an arithmetic circuit
- And then represented the *shape* of that circuit as the polynomial $P=12x^2-3x-9 = x^2-3x+2$

## Where we are going
- Given a 256-bit private key, one could construct a very long equation whose only (known) solution is that key
- Then convert that into a (huge) arithmetic circuit
- And then represent it as a polynomial $P$
- If Alice could prove to Bob that she knew such a polynomial...
  - Using homomorphic hidings, so zero information is revealed
  - And in such a way that could be verified
- Then Bob would know that Alice really knew her private key

## What we have
- Alice has polynomial $P$
  - $P$ represents an arithmetic circuit that represents an equation that she has a satisfying assignment for
  - $P$ is a sum of the smaller polynomials $L$, $R$, and $O$
- We also have a *target polynomial* $T$ which divides $P$
  - If $T$ divides $P$, then we can state that $P=H \cdot T$ for some $H$
  - Note that $T$ is know to all parties, as it is part of the agreed-upon algorithm

## If Alice is faking it
- Suppose that Alice does *not* have a satisfying assignment $(c_1,...,c_m)$, but still tries to construct the circuit and then $P$
- Then $T$, which is known to all parties, will not divide $P$
  - You can't make up a polynomial such that $P=H \cdot T$ without brute forcing it
- This means that $H$ (the correct polynomial) and $H'$ (the "faked" polynomial) must be different polynomials

## ZK Verification Protocol
1. Alice computes $P$ (from $L$, $R$, and $O$), and $H$ (from $P=H \cdot T$), from the circuit from the equation she is trying to satisfy
2. Bob chooses a random value $x \in Z_p$
   - He sends the necessary homomorphic hidings to Alice so she can evaluate those four polynomials
   - He also computes $E(T(x))$, but does not send this to Alice

## ZK Verification Protocol
3. Alice sends Bob the hidings of these polynomials evaluated at $x$
   - Specifically: $E(L(x))$, $E(R(x))$, $E(O(x))$, and $E(H(x))$
   - Something called a random $T$-shift happens to ensure zero-knowledge
4. Bob checks if this equation holds at $x$
   - Only he knows $E(T(x))$, and thus he can verify that $E(L(x) \cdot R(x) - O(x))=E(T(x) \cdot H(x))$

## Problem
- For this verification to happen, Bob must compute:

$$E(L(x) \cdot R(x) - O(x))=E(T(x) \cdot H(x))$$

- But our homomorphic hiding operation $E(x)$ does not support multiplication by a non-scalar
- If it did, then we could get this whole thing working properly
- Solution: elliptic curves!
- We also want to make this non-interactive
  - More on that shortly

## Ideal non-interactiveness
- A prover broadcasts a message to all parties
- Anybody can read this message and verify the claim
- It turns out this is impossible to do so and also remain zero-knowledge

## Practical non-interactiveness
- We establish a Common Reference System (CRS)
  - A series of random values to be used in the zero-knowledge proof
- These values are broadcast to all parties
- We assume that the randomness for this is not known to any party
  - Knowledge of such could allow for false claims

## Previous protocol
- Recall the previous interactive protocol:
  1. Given an agreed-upon $E(x)$ (with a $g$ therein), Bob chooses a random $\alpha,x \in Z_p$, and sends Alice the hidings of $g,x \cdot g,\ldots,x^d \cdot g$ and also $\alpha \cdot g,\alpha x \cdot g,\ldots,\alpha x^d \cdot g$
  2. Alice computes $a=E(P(x))$ and $b=E(\alpha P(x))$ using those values, and sends that to Bob
     - Her computation is based on her polynomial $P$ and thus $L$, $R$, and $O$
  3. Bob checks that $b = \alpha \cdot a$, and accepts only if true

## Non-interactive algorithm
- The CRS chooses a random $\alpha,x \in Z_p$, but *does not publish them*
  - It does publish the hidings: $(E(1),E(x),\ldots,E(x^d))$ and $(E(\alpha),E(\alpha x),\ldots,E(\alpha x^d))$
  - This is a fair amount of data, but it's used by *all* the zero knowledge provers in that block
- Alice computes $a=E(P(x))$ and $b=E(\alpha P(x))$
  - She publishes this for later verification
  - This is only two 256-bit values
- For Bob to verify:
  - Compute $E(\alpha x) = \text{Tate}(E(P(x)),E(\alpha))$
  - Verify that Alice's provided $b=E(\alpha P(x))$ equals what we computed

Zcash

## [![zec logo](../slides/images/logos/zec-coin-symbol.svg)](https://coinmarketcap.com/currencies/zcash/) Zcash (ZEC)
- Website: https://z.cash
  - Blockchain explorer: https://blockchair.com/zcash/
- Source code fork of Bitcoin
  - So it's useful for transactions, but not smart contracts
  - Available online at https://github.com/zcash/zcash
- PoW hash function: [Equihash](https://en.wikipedia.org/wiki/Equihash)
- Development started in 2013
  - First mined in 2016
- [Whitepaper](https://zips.z.cash/protocol/protocol.pdf)

## History
- [Zerocoin protocol](https://en.wikipedia.org/wiki/Zerocoin_protocol) was developed by [Professor Matthew Green @ JHU](https://isi.jhu.edu/~mgreen/)
  - An extension to Bitcoin that adds zk-SNARKs
  - Not compatible with regular Bitcoin, though
- Zcash was the first coin that merged the Zerocoin protocol and Bitcoin
  - Developed by Green and his graduate students
- Now managed by the Zcash Foundation and the Electric Coin Company

## The Ceremony
- Need to start with a very random seed!
  - Each successive seed could use the previous block's hash, which is not predictable
- Two-day process involving multiple people and computers
  - Each successive person didn't know who was the next in line
- The computers involved were reportedly destroyed
- [Radiolab podcast about The Ceremony](https://www.wnycstudios.org/podcasts/radiolab/articles/ceremony) (Feb 25, 2021 episode)

## Two Address Types
- "Regular" or "Traceable" addresses
  - Traceable like Bitcoin is traceable
  - Called a $t$-address, and starts with a 't'
- "Shielded" addresses
  - Shielded by a zk-SNARK
  - Called a $z$-address, and starts with a 'z'
  - Can selectively share *some* information for auditing purposes

## Four Transaction Types
- Z-to-Z: Private transaction
  - It's know to have occurred, but the information is not publicly visible
- T-to-T: Public transaction
  - Just like Bitcoin, it's traceable
- Z-to-T: Deshielding transaction
  - The recipient (only) is known, and it's known that it came from a $z$-address
- T-to-Z: Shielding transaction
  - The sender (only) is known, and it's known that it went to a $z$-address

## Zcash protocol
- UTXOs are called *commitments*
  - To spend a commitment, we reveal a *nullifier*
  - Both are stored as hashes
- For each shielded transaction, the sender publishes:
  - $commitment = \text{hash}(addr,amt,rho)$
    - $addr$ is the recipient address
    - $amt$ is the amount to transfer
    - $rho$ is a unique value for this Tx
    - (we are ignoring the nonce)
- To spend a commitment, the spender publishes:
  - $nullifier = \text{hash}(pkey,rho)$
    - Where $pkey$, the private key, can be used to derive $addr$, the account address

## How to verify?
- $commitment = \text{hash}(addr,amt,rho)$
- $nullifier = \text{hash}(pkey,rho)$
- Create an arbitrary computation that shows:
  - The spender knows $addr$, $amt$, $rho$, and $pkey$
  - The hash of *commitment* can be computed based on $addr$, $amt$, and $rho$
  - The hash of *nullifier* can be computed based on $pkey$ and $rho$
- Then verify this via a zk-SNARK

<img src="https://z.cash/wp-content/uploads/2021/07/featured-wallet-502x1024.png" style="background:transparent">

## Mobile wallet
- Zecwallet Lite
  - Download from [zecwallet.co](https://www.zecwallet.co/)
- Supports transactions to and from both shielded and transparent addresses
- Lite version also available for the desktop
- Image from [here](https://z.cash/wallets/)

## Desktop wallet

- Runs a full node in the P2P cryptocurrency network
  - Just like when we run a geth node
  - To get *incoming* connections, you have to open a port on your router
- Image from [here](https://www.zecwallet.co/fullnode.html)

Firo (aka Zcoin)

## [![firo logo](../slides/images/logos/firo-coin-symbol.svg)](https://coinmarketcap.com/currencies/firo/) Firo (FIRO)
- Website: https://firo.org/
  - Blockchain explorer: https://explorer.firo.org/
- Previously known as Zcoin
  - Name changed to Firo in October 2020
- Also created at JHU, also based on the Bitcoin source code
- Also used the Zerocoin protocol
  - Now uses a different protocol called "Sigma"
- PoW hash function: Merkle Tree Proof
- Development started in 2014
  - First mined in 2016
- [Whitepaper](https://lelantus.io/enabling-untraceable-anonymous-payments.pdf)

## History
- Started via a Masters paper in 2014; first mined in 2016
  - By the same research group at JHU
- Sep 2018: can use TOR or VPN to hide your origin IP
- Dec 2018: mining algorithm changed to Merkle Tree proof
  - More memory intensive, so less likely to be viable by ASICs
- Jan 2020: implemented Receiver Address Privacy (RAP)
  - Single receiving address, but outsiders cannot view transaction history
- Aug 2021: the Lelantus Spark protocol adds even more privacy features

## Notable Incidents
- A single-character programming error allowed the creation of 370k fake coins in February 2017
  - Woth `$`440k at the time
- Flaw in Zerocoin discovered and patched in April 2018 (no known exploits)
- First large-scale blockchain elections for the Thailand Democratic Party in November 2018
- Suffered a 51% attack in Jan 2021

## Desktop wallet

- Similar in look to the Bitcoin core wallet
- Note the 'anonymize all' button
  - Converts "transparent" balances to "private" balances
  - Similar to Zcash
- Notice the "anonymous communication with Tor" check box
- Image adapted from [here](https://en.wikipedia.org/wiki/File:Firo_Core_wallet_GUI_0.14.6.0_on_Windows_10.png)